解:(1)由动点C满足

=t
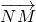
,知点C的轨迹是M、N两点所在的直线,
又因为直线MN的方程为x-y-4=0
∴点C的轨迹方程为x-y-4=0
设A(x
1,y
1),B(x
2,y
2)
由
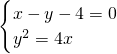
得:
x
2-12x+16=0
∴x
1•x
2=16,x
1+x
2=12
又y
1•y
2=(x
1-4)•(x
2-4)=-16
∴x
1•x
2+y
1•y
2=0
∴

⊥

;
(2)假设存在P(m,0)(m≠0),使得过点P的直线l交抛物线y
2=4x 于D,E两点,并以线段DE为直径的圆都过原点,
由题意知:弦所在的直线的斜率不为零.故设弦所在的直线方程为:x=ky+m,
代入 y
2=4x 得 y
2-4ky-4m=0,设D(x
1,y
1),E(x
2,y
2)
∴y
1+y
2=4k,y
1y
2=-4m.
若以弦DE为直径的圆都过原点,则OD⊥OE,∴x
1x
2+y
1y
2=0.
即
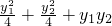
=m
2-4m,解得m=0 (不合题意,舍去)或 m=4.
∴存在点P(4,0),使得过P点任作抛物线的一条弦,以该弦为直径的圆都过原点.
设弦D,E的中点为M(x,y)
则x=

(x
1+x
2),y=

( y
1+y
2)=2k,
x
1+x
2=ky
1+4+ky
2+4=k(y
1+y
2)+8=4k
2+8,
∴x=2k
2+4,y=2k,
∴消去k得弦D,E的中点M的轨迹方程为:y
2=2x-8.
∴圆心的轨迹方程为y
2=2x-8.
分析:(1)欲证两向量垂直,通过向量的坐标运算,就是证明它们的数量积为0,将直线与抛物线的方程组成方程组,利用设而不求的方法求解;
(2)对于存在性问题,可设假设存在,本题中将垂直关系合理转化,找出m的一个相等关系,从而解出了m的值,即说明存在.
点评:本题主要考查了直线与圆锥曲线的综合问题及存在性问题.对于存在判断型问题,解题的策略一般为先假设存在,然后转化为“封闭型”问题求解判断,若不出现矛盾,则肯定存在;若出现矛盾,则否定存在.这是一种最常用也是最基本的方法,解圆锥曲线的中点弦问题的一般方法是:联立直线和圆锥曲线的方程,借助于一元二次方程的根的判别式、根与系数的关系、中点坐标公式及参数法求解.

 =t
=t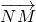 且点C的轨迹与抛物线y2=4x交于A,B两点.
且点C的轨迹与抛物线y2=4x交于A,B两点. ⊥
⊥ ;
; =t
=t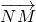 ,知点C的轨迹是M、N两点所在的直线,
,知点C的轨迹是M、N两点所在的直线,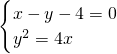 得:
得: ⊥
⊥ ;
;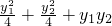 =m2-4m,解得m=0 (不合题意,舍去)或 m=4.
=m2-4m,解得m=0 (不合题意,舍去)或 m=4. (x1+x2),y=
(x1+x2),y= ( y1+y2)=2k,
( y1+y2)=2k,

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案