
【题目】已知函数![]() ,其中
,其中![]() .
.
(1)若![]() 在
在![]() 上存在极值点,求
上存在极值点,求![]() 的取值范围;
的取值范围;
(2)设![]() ,
, ![]() ,若
,若![]() 存在最大值,记为
存在最大值,记为![]() ,则当
,则当![]() 时,
时, ![]() 是否存在最大值?若存在,求出其最大值;若不存在,请说明理由.
是否存在最大值?若存在,求出其最大值;若不存在,请说明理由.
【答案】(1)![]() ;(2)存在,且
;(2)存在,且![]() 存在最大值为
存在最大值为![]() .
.
【解析】试题分析:
(1)函数存在极值点,将问题转化为导函数有根,且不为重根,据此分离系数,结合对勾函数的性质和函数的定义域求解实数![]() 的取值范围即可;
的取值范围即可;
(2)分类讨论,当![]() 时,
时, ![]() 不存在最大值,
不存在最大值,
当![]() 时,由根与系数的关系求得
时,由根与系数的关系求得![]() 的解析式,结合
的解析式,结合![]() 的式子构造新函数
的式子构造新函数![]() ,利用新函数的性质结合题意即可求得
,利用新函数的性质结合题意即可求得![]() 的最大值.
的最大值.
解:
(1)![]() ,
, ![]() .
.
由题意,得![]() ,在
,在![]() 上有根(不为重根).
上有根(不为重根).
即![]() 在
在![]() 上有解.
上有解.
由![]() 在
在![]() 上单调递增,得
上单调递增,得![]() .
.
检验:当![]() 时,
时, ![]() 在
在![]() 上存在极值点.
上存在极值点.
∴![]() .
.
(2)若![]() ,∵
,∵![]() 在
在![]() 上满足
上满足![]() ,
,
∴![]() 在
在![]() 上单调递减,∴
上单调递减,∴![]() .
.
∴![]() 不存在最大值.
不存在最大值.
则![]() .
.
∴方程![]() 有两个不相等的正实数根,令其为
有两个不相等的正实数根,令其为![]() ,且不妨设
,且不妨设![]()
则![]() .
.
![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上调递增,在
上调递增,在![]() 上单调递减,
上单调递减,
对![]() ,有
,有![]() ;对
;对![]() ,有
,有![]() ,
,
∴![]() .
.
∴![]()
![]() .
.
将![]() ,
, ![]() 代入上式,消去
代入上式,消去![]() 得
得
![]()
∵![]() ,∴
,∴![]() ,
, ![]() .
.
据![]() 在
在![]() 上单调递增,得
上单调递增,得![]() .
.
设![]() ,
, ![]() .
.
![]() ,
, ![]() .
.
∴![]() ,即
,即![]() 在
在![]() 上单调递增.
上单调递增.
∴![]()
∴![]() 存在最大值为
存在最大值为![]() .
.


科目:高中数学 来源: 题型:
【题目】某市春节期间7家超市的广告费支出![]() (万元)和销售额
(万元)和销售额![]() (万元)数据如下:
(万元)数据如下:
超市 | A | B | C | D | E | F | G |
广告费支出 | 1 | 2 | 4 | 6 | 11 | 13 | 19 |
销售额 | 19 | 32 | 40 | 44 | 52 | 53 | 54 |
(1)若用线性回归模型拟合![]() 与
与![]() 的关系,求
的关系,求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)用二次函数回归模型拟合![]() 与
与![]() 的关系,可得回归方程:
的关系,可得回归方程:![]() ,
,
经计算二次函数回归模型和线性回归模型的![]() 分别约为
分别约为![]() 和
和![]() ,请用
,请用![]() 说明选择哪个回归模型更合适,并用此模型预测
说明选择哪个回归模型更合适,并用此模型预测![]() 超市广告费支出为3万元时的销售额.
超市广告费支出为3万元时的销售额.
参数数据及公式:![]() ,
,![]() ,
,
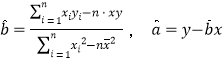 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某运动员每次投篮命中的概率低于![]() ,现采用随机模拟的方法估计该运动员三次投篮恰有两次命中的概率:先由计算器产生0到9之间取整数值的随机数,指定1,2,3,4表示命中,5,6,7,8,9,0表示不命中;再以每三个随机数为一组,代表三次投篮的结果,经随机模拟产生了如下20组随机数:
,现采用随机模拟的方法估计该运动员三次投篮恰有两次命中的概率:先由计算器产生0到9之间取整数值的随机数,指定1,2,3,4表示命中,5,6,7,8,9,0表示不命中;再以每三个随机数为一组,代表三次投篮的结果,经随机模拟产生了如下20组随机数:
907 966 191 925 271 932 812 458 569 683
431 257 393 027 556 488 730 113 537 989
据此估计,该运动员三次投篮恰有两次命中的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个盒子里装有三张卡片,分别标记有数字1,2,3,这三张卡片除标记的数字外完全相同.随机有放回地抽取3次,每次抽取1张,将抽取的卡片上的数字依次记为a,b,c.求:
(1)“抽取的卡片上的数字满足a+b=c”的概率;
(2)“抽取的卡片上的数字a,b,c不完全相同”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设甲、乙、丙3个乒乓球协会的运动员人数分别为27,9,18.现采用分层抽样的方法从这3个协会中抽取6名运动员组队参加比赛.
(1)求应从这3个协会中分别抽取的运动员的人数.
(2)将抽取的6名运动员进行编号,编号分别为A1,A2,A3,A4,A5,A6.现从这6名运动员中随机抽取2人参加双打比赛.
①用所给编号列出所有可能的结果;
②设事件A为“编号为A5和A6的2名运动员中至少有1人被抽到”,求事件A发生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2015年7月9日21时15分,台风“莲花”在我国广东省陆丰市甲东镇沿海登陆,给当地人民造成了巨大的财产损失,适逢暑假,小张调查了当地某小区的100户居民由于台风造成的经济损失,将收集的数据分成![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 五组,并作出如下频率分布直方图(图1):
五组,并作出如下频率分布直方图(图1):
(Ⅰ)台风后居委会号召小区居民为台风重灾区捐款,小张调查的100户居民捐款情况如右下表格,在图2表格空白处填写正确数字,并说明是否有![]() 以上的把握认为捐款数额多于或少于500元和自身经济损失是否到4000元有关?
以上的把握认为捐款数额多于或少于500元和自身经济损失是否到4000元有关?


(Ⅱ)将上述调查所得到的频率视为概率. 现在从该地区大量受灾居民中,采用随机抽样方法每次抽取1户居民,抽取3次,记被抽取的3户居民中自身经济损失超过4000元的人数为![]() . 若每次抽取的结果是相互独立的,求
. 若每次抽取的结果是相互独立的,求![]() 的分布列,期望
的分布列,期望![]() 和方差
和方差![]() .
.
附:临界值表
| 0.10 | 0.05 | 0.025 |
| 2.706 | 3.841 | 5.024 |
随机量变

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题正确的是__________.(写出所有正确命题的序号)
①已知![]() ,“
,“![]() 且
且![]() ”是“
”是“![]() ”的充要条件;
”的充要条件;
②已知平面向量![]() ,“
,“![]() 且
且![]() ”是“
”是“![]() ”的必要不充分条件;
”的必要不充分条件;
③已知![]() ,“
,“![]() ”是“
”是“![]() ”的充分不必要条件;
”的充分不必要条件;
④命题![]() :“
:“![]() ,使
,使![]() 且
且![]() ”的否定为
”的否定为![]() :“
:“![]() ,都有
,都有![]() 且
且![]() ”
”
查看答案和解析>>
科目:高中数学 来源: 题型:
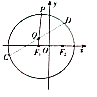
【题目】一张半径为4的圆形纸片的圆心为![]() ,
, ![]() 是圆内一个定点,且
是圆内一个定点,且![]() ,
, ![]() 是圆上一个动点,把纸片折叠使得
是圆上一个动点,把纸片折叠使得![]() 与
与![]() 重合,然后抹平纸片,折痕为
重合,然后抹平纸片,折痕为![]() ,设
,设![]() 与半径
与半径![]() 的交点为
的交点为![]() ,当
,当![]() 在圆上运动时,则
在圆上运动时,则![]() 点的轨迹为曲线
点的轨迹为曲线![]() ,以
,以![]() 所在直线
所在直线![]() 为轴,
为轴, ![]() 的中垂线为
的中垂线为![]() 轴建立平面直角坐标系,如图.
轴建立平面直角坐标系,如图.
(1)求曲线![]() 的方程;
的方程;
(2)曲线![]() 与
与![]() 轴的交点为
轴的交点为![]() ,
, ![]() (
(![]() 在
在![]() 左侧),与
左侧),与![]() 轴不重合的动直线
轴不重合的动直线![]() 过点
过点![]() 且与
且与![]() 交于
交于![]() 、
、![]() 两点(其中
两点(其中![]() 在
在![]() 轴上方),设直线
轴上方),设直线![]() 、
、![]() 交于点
交于点![]() ,求证:动点
,求证:动点![]() 恒在定直线
恒在定直线![]() 上,并求
上,并求![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地政府拟在该地一水库上建造一座水电站,用泄流水量发电.下图是根据该水库历年的日泄流量的水文资料画成的日泄流量X(单位:万立方米)的频率分布直方图(不完整),已知![]() ,历年中日泄流量在区间[30,60)
,历年中日泄流量在区间[30,60)
的年平均天数为156,一年按364天计.
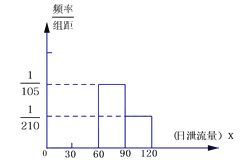
(Ⅰ)请把频率分布直方图补充完整;
(Ⅱ)该水电站希望安装的发电机尽可能运行,但每30万立方米的日泄流量才够运行一台发电机,如![]() 时才够运行两台发电机,若运行一台发电机,每天可获利润为4000元,若不运行,则该台发电机每天亏损500元,以各段的频率作为相应段的概率,以水电站日利润的期望值为决策依据,问:为使水电站日利润的期望值最大,该水电站应安装多少台发电机?
时才够运行两台发电机,若运行一台发电机,每天可获利润为4000元,若不运行,则该台发电机每天亏损500元,以各段的频率作为相应段的概率,以水电站日利润的期望值为决策依据,问:为使水电站日利润的期望值最大,该水电站应安装多少台发电机?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com