
【题目】已知函数![]() 是定义在
是定义在![]() 上的偶函数,且
上的偶函数,且![]() ,当
,当![]() 时,
时,![]() .
.
(1)求函数![]() 的解析式;
的解析式;
(2)解不等式![]() .
.
【答案】(1) 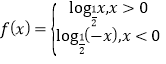 ;(2)
;(2)![]() .
.
【解析】
(1)设![]() ,可得
,可得![]() ,则
,则![]() ,再由函数
,再由函数![]() 是偶函数求出
是偶函数求出![]() 的解析式,即可求得结论;(2)由
的解析式,即可求得结论;(2)由![]() 是偶函数,不等式
是偶函数,不等式![]() 可化为
可化为![]() ,利用函数
,利用函数![]() 在
在![]() 上是减函数,可得
上是减函数,可得![]() ,求解绝对值的不等式,可得原不等式的解集.
,求解绝对值的不等式,可得原不等式的解集.
(1)当x<0时,-x>0,则f(-x)=log![]() (-x).
(-x).
因为函数f(x)是偶函数,所以f(-x)=f(x)=log![]() (-x),
(-x),
所以函数f(x)的解析式为
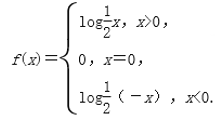
(2)因为f(4)=log![]() 4=-2,f(x)是偶函数,
4=-2,f(x)是偶函数,
所以不等式f(x2-1)>-2转化为f(|x2-1|)>f(4).
又因为函数f(x)在(0,+∞)上是减函数,
所以|x2-1|<4,解得-![]() <x<
<x<![]() ,
,
即不等式的解集为(-![]() ,
,![]() ).
).


 考前必练系列答案
考前必练系列答案科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC﹣A1B1C1中,侧面AA1B1B⊥底面ABC,△ABC和△ABB1都是边长为2的正三角形. 
(Ⅰ)过B1作出三棱柱的截面,使截面垂直于AB,并证明;
(Ⅱ)求AC1与平面BCC1B1所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知过抛物线G:y2=2px(p>0)焦点F的直线l与抛物线G交于M、N两点(M在x轴上方),满足 ![]() ,
, ![]() ,则以M为圆心且与抛物线准线相切的圆的标准方程为( )
,则以M为圆心且与抛物线准线相切的圆的标准方程为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017年3月智能共享单车项目正式登陆某市,两种车型![]() “小绿车”、“小黄车”
“小绿车”、“小黄车”![]() 采用分时段计费的方式,“小绿车”每30分钟收费
采用分时段计费的方式,“小绿车”每30分钟收费![]() 元
元![]() 不足30分钟的部分按30分钟计算
不足30分钟的部分按30分钟计算![]() ;“小黄车”每30分钟收费1元
;“小黄车”每30分钟收费1元![]() 不足30分钟的部分按30分钟计算
不足30分钟的部分按30分钟计算![]() 有甲、乙、丙三人相互独立的到租车点租车骑行
有甲、乙、丙三人相互独立的到租车点租车骑行![]() 各租一车一次
各租一车一次![]() 设甲、乙、丙不超过30分钟还车的概率分别为
设甲、乙、丙不超过30分钟还车的概率分别为![]() ,
,![]() ,
,![]() ,三人租车时间都不会超过60分钟
,三人租车时间都不会超过60分钟![]() 甲、乙均租用“小绿车”,丙租用“小黄车”.
甲、乙均租用“小绿车”,丙租用“小黄车”.
![]() 求甲、乙两人所付的费用之和等于丙所付的费用的概率;
求甲、乙两人所付的费用之和等于丙所付的费用的概率;
![]() 2
2![]() 设甲、乙、丙三人所付的费用之和为随机变量
设甲、乙、丙三人所付的费用之和为随机变量![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn , Sn=2an﹣1,{bn}是等差数列,且b1=a1 , b4=a3 .
(1)求数列{an}和{bn}的通项公式;
(2)若 ![]() ,求数列{cn}的前n项和Tn .
,求数列{cn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知点D为三角形ABC边BC上一点, ![]() =3
=3 ![]() ,En(n∈N*)为AC边上的一列点,满足
,En(n∈N*)为AC边上的一列点,满足 ![]() =
= ![]() an+1
an+1 ![]() ﹣(3an+2)
﹣(3an+2) ![]() ,其中实数列{an}中,an>0,a1=1,则{an}的通项公式为( )
,其中实数列{an}中,an>0,a1=1,则{an}的通项公式为( ) 
A.32n﹣1﹣1
B.2n﹣1
C.3n﹣2
D.23n﹣1﹣1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)(x∈R)满足f(﹣x)=4﹣f(x),函数 ![]() ,若曲线y=f(x)与y=g(x)图象的交点分别为(x1 , y1),(x2 , y2),(x3 , y3),…,(xm , ym),则
,若曲线y=f(x)与y=g(x)图象的交点分别为(x1 , y1),(x2 , y2),(x3 , y3),…,(xm , ym),则 ![]() (结果用含有m的式子表示).
(结果用含有m的式子表示).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com