
平行四边形ABCD中,AB=2,AD=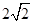 ,且
,且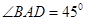 ,以BD为折线,把
,以BD为折线,把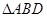 折起,使平面
折起,使平面 ,连AC。(1)求异面直线AD与BC所成角大小;(2)求二面角B-AC-D平面角的大小;(3)求四面体ABCD外接球的体积。
,连AC。(1)求异面直线AD与BC所成角大小;(2)求二面角B-AC-D平面角的大小;(3)求四面体ABCD外接球的体积。

(1)异面直线AD与BC所成角为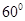 (2)二面角B-AC-D的大小是
(2)二面角B-AC-D的大小是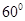 ;
;
(3)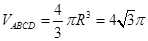 。
。
【解析】本试题主要是考查了立体几何中异面直线所成的角和二面角的大小以及球的体积的求解的综合运用。
(1)在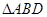 中,
中,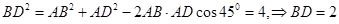 ,易得
,易得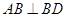 ,
,
在四面体ABCD中,以D为原点,DB为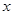 轴,DC为
轴,DC为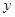 轴,过D垂直于平面BDC的射线为
轴,过D垂直于平面BDC的射线为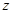 轴,建立如图空间直角坐标系,那么利用向量的夹角得到异面直线的角。
轴,建立如图空间直角坐标系,那么利用向量的夹角得到异面直线的角。
(2)利用法向量与法向量的夹角得到二面角的平面角。
(3)由于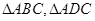 均为直角三角形,故四面体ABCD的外接球球心在AD中点,
均为直角三角形,故四面体ABCD的外接球球心在AD中点,
又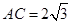 ,所以球半径
,所以球半径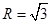 ,从而得到结论。
,从而得到结论。
解:在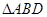 中,
中,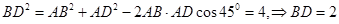 ,易得
,易得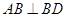 ,
,
在四面体ABCD中,以D为原点,DB为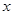 轴,DC为
轴,DC为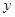 轴,过D垂直于平面BDC的射线为
轴,过D垂直于平面BDC的射线为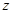 轴,建立如图空间直角坐标系。
轴,建立如图空间直角坐标系。
|
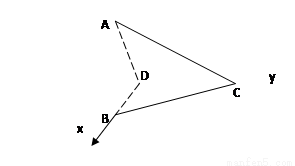
则D(0,0,0),B(2,0,0),C(0,2,0),A(2,0,2)
(1)由于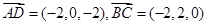 ,设AD与BC所成角为
,设AD与BC所成角为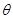 ,则
,则
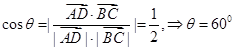 ,即异面直线AD与BC所成角为
,即异面直线AD与BC所成角为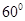
(2)设平面ABC的法向量为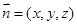 ,而
,而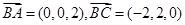 ,
,
由 得:
得: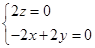 ,取
,取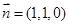 。
。
再设平面DAC的法向量为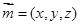 ,而
,而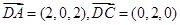 ,
,
由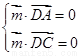 得:
得: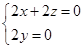 ,取
,取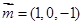 ,
,
所以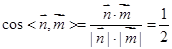 ,所以二面角B-AC-D的大小是
,所以二面角B-AC-D的大小是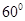
(3)……由于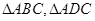 均为直角三角形,故四面体ABCD的外接球球心在AD中点,
均为直角三角形,故四面体ABCD的外接球球心在AD中点,
又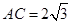 ,所以球半径
,所以球半径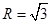 ,得
,得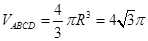 。
。


科目:高中数学 来源: 题型:
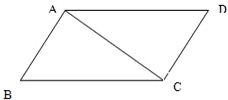 如图,在平行四边形ABCD中,AB=AC=1,∠ACD=90°,将它沿对角线AC折起,使AB与CD成60°角,则此时B、D的距离是 ( )
如图,在平行四边形ABCD中,AB=AC=1,∠ACD=90°,将它沿对角线AC折起,使AB与CD成60°角,则此时B、D的距离是 ( )A、2或
| ||
B、2或
| ||
| C、2 | ||
D、1或
|
查看答案和解析>>
科目:高中数学 来源: 题型:
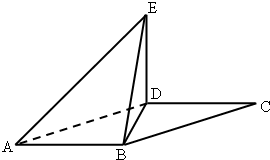 如图,平行四边形ABCD中,∠DAB=60°,AB=2,AD=4将△CBD沿BD折起到△EBD的位置,使平面EDB⊥平面ABD.
如图,平行四边形ABCD中,∠DAB=60°,AB=2,AD=4将△CBD沿BD折起到△EBD的位置,使平面EDB⊥平面ABD.查看答案和解析>>
科目:高中数学 来源: 题型:
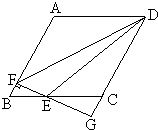 如图,在平行四边形ABCD中,AB=4,BC=3,∠BAD=120°,E为BC上一动点(不与B重合),作EF⊥AB于F,FE的延长线交DC的延长线于点G,设BE=x,△DEF的面积为S.
如图,在平行四边形ABCD中,AB=4,BC=3,∠BAD=120°,E为BC上一动点(不与B重合),作EF⊥AB于F,FE的延长线交DC的延长线于点G,设BE=x,△DEF的面积为S.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com