
【题目】已知首项为![]() 的数列
的数列![]() 各项均为正数,且
各项均为正数,且![]() ,
,![]() .
.
(1)若数列![]() 的通项
的通项![]() 满足
满足![]() ,且
,且![]() ,求数列
,求数列![]() 的前n项和为
的前n项和为![]() ;
;
(2)若数列![]() 的通项
的通项![]() 满足
满足 ,前n项和为
,前n项和为![]() ,当数列
,当数列![]() 是等差数列时,对任意的
是等差数列时,对任意的![]() ,均存在
,均存在![]() ,使得
,使得![]() 成立,求满足条件的所有整数
成立,求满足条件的所有整数![]() 构成的集合.
构成的集合.
【答案】(1)![]() ;(2)
;(2) .
.
【解析】
(1)由条件可变形为![]() ,可得数列
,可得数列![]() 是以
是以![]() 为首项,以2为公比的等比数列,进而可得
为首项,以2为公比的等比数列,进而可得![]() ,则
,则![]() ,再利用错位相减法求和即可;
,再利用错位相减法求和即可;
(2)根据(1)求出![]() ,
,![]() ,
,![]() ,由数列
,由数列![]() 是等差数列,列方程可得
是等差数列,列方程可得![]() 或
或![]() ,分
,分![]() 和
和![]() 讨论,通过条件对任意的
讨论,通过条件对任意的![]() ,均存在
,均存在![]() ,使得
,使得![]() 成立,可得
成立,可得![]() .
.
(1)∵数列![]() 各项均为正数,且
各项均为正数,且![]() ,
,
![]() ,即
,即![]() ,即
,即![]() .
.
∴数列![]() 是以
是以![]() 为首项,以2为公比的等比数列,
为首项,以2为公比的等比数列,
![]() ,
,
∴数列![]() 的通项公式为
的通项公式为![]() .
.
∵![]() ,∴
,∴![]() ,
,
∴![]() ,
,
![]() ,
,
两式相减,得![]()
![]()
![]() ,
,
![]() ,
,
∴数列![]() 的前n项和
的前n项和![]() ;
;
(2)∵数列![]() 的通项
的通项 ,
,
∴由(1)得, ,∴
,∴![]() ,
,![]() ,
,![]() .
.
又数列![]() 是等差数列,∴
是等差数列,∴![]() .
.
![]() ,即
,即![]() .
.
解得![]() 或
或![]() .
.
又 ,
,
∴当![]() 时,
时,![]() ,
,![]() 为等差数列,
为等差数列,

![]()
对任意的![]() ,均存在
,均存在![]() ,使得
,使得![]() 成立,
成立,
![]() ,
,
![]() ,
,![]() .
.
又![]() 为正整数,∴满足条件的所有整数
为正整数,∴满足条件的所有整数![]() 的值构成的集合为
的值构成的集合为
 .
.
当![]() 时,
时,![]() ,
,![]() 不是常数,
不是常数,
∴数列![]() 不是等差数列,舍去.
不是等差数列,舍去.
综上,满足条件的所有整数![]() 的值构成的集合为
的值构成的集合为
 .
.


 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案科目:高中数学 来源: 题型:
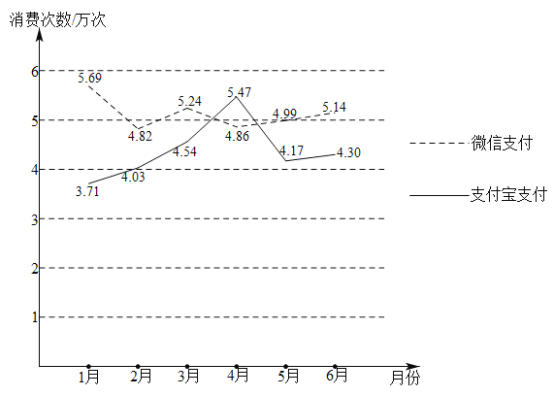
【题目】某超市为了了解“微信支付”与“支付宝支付”的情况(“微信支付”与“支付宝支付”统称为“移动支付”),对消费者在该超市在2019年1-6月的支付方式进行统计,得到如图所示的折线图,则下列判断正确的是( )
①这6个月中使用“微信支付”的总次数比使用“支付宝支付”的总次数多
②这6个月中使用“微信支付”的消费总额比使用“支付宝支付”的消费总额大
③这6个月中4月份平均每天使用“移动支付”的次数最多
④2月份平均每天使用“移动支付”比5月份平均每天使用“移动支付”的次数多
A.①③B.①②③C.①③④D.①②③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正三棱柱ABCA1B1C1中,已知AB=1,AA1=2,E,F,G分别是棱AA1,AC和A1C1的中点,以![]() 为正交基底,建立如图所示的空间直角坐标系F-xyz.
为正交基底,建立如图所示的空间直角坐标系F-xyz.

(1)求异面直线AC与BE所成角的余弦值;
(2)求二面角F-BC1-C的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C:![]() (
(![]() )的焦点F到准线l的距离为2,直线
)的焦点F到准线l的距离为2,直线![]() 过点F且与抛物线交于M、N两点,直线
过点F且与抛物线交于M、N两点,直线![]() 过坐标原点O及点M且与l交于点P,点Q在线段
过坐标原点O及点M且与l交于点P,点Q在线段![]() 上.
上.
(1)求直线![]() 的斜率;
的斜率;
(2)若![]() ,
,![]() ,
,![]() 成等差数列,求点Q的轨迹方程.
成等差数列,求点Q的轨迹方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,将![]() 方格纸中每个小方格染三种颜色之一,使得每种颜色的小方格的个数相等.若相邻两个小方格的颜色不同,称他们的公共边为“分割边”,则分割边条数的最小值为( )
方格纸中每个小方格染三种颜色之一,使得每种颜色的小方格的个数相等.若相邻两个小方格的颜色不同,称他们的公共边为“分割边”,则分割边条数的最小值为( )

A.33B.56C.64D.78
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,
的中点,![]() ,如图1.以
,如图1.以![]() 为折痕将
为折痕将![]() 折起,使点
折起,使点![]() 到达点
到达点![]() 的位置,如图2.
的位置,如图2.
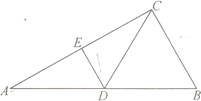

如图1 如图2
(1)证明:平面![]() 平面
平面![]() ;
;
(2)若平面![]() 平面
平面![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值。
所成角的正弦值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某民航部门统计的2019年春运期间12个城市售出的往返机票的平均价格以及相比上年同期变化幅度的数据统计图表如图所示,根据图表,下面叙述不正确的是( )
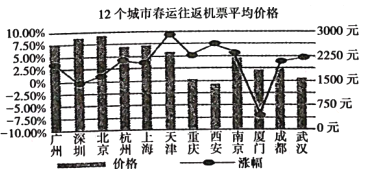
A. 同去年相比,深圳的变化幅度最小且厦门的平均价格有所上升
B. 天津的平均价格同去年相比涨幅最大且2019年北京的平均价格最高
C. 2019年平均价格从高到低居于前三位的城市为北京、深圳、广州
D. 同去年相比,平均价格的涨幅从高到低居于前三位的城市为天津、西安、南京
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]()
![]() 经过点
经过点![]() ,离心率为
,离心率为![]() ,过点
,过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]() ,
,
(1)求椭圆![]() 的方程;
的方程;
(2)求![]() 的取值范围;
的取值范围;
(3)设直线![]() 和
和![]() 的斜率分别为
的斜率分别为![]() 和
和![]() ,求证:
,求证:![]() 为定值.
为定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com