
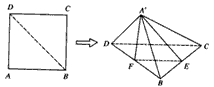
| (Ⅰ)根据题意,有平面A′BD⊥平面BCD,A′F⊥BD于F,A′D= A′B, ∴F为BD的中点, 又E为BC的中点, ∴EF∥CD, ∴EF∥平面A′CD。 (Ⅱ)∵平面A′BD⊥平面BCD,A′F⊥BD, ∴A′F⊥平面BCD, ∴∠A′EF为直线A′E与平面BCD所成的角, 设正方形ABCD边长为a,则  , ,∴  , ,∴直线A′E与平面BCD所成角的余弦值为 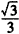 。 。 |
|
(Ⅲ)连结FC,有 ,∴ ,∴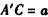 , , ∴A′B=BC=A′C=A′D=CD=a, 取A′C的中点为M,则BM⊥A′C,DM⊥A′C, ∴∠BMD为二面角B-A′C-D的平面角, ∵△A′BC和△A′DC都为正三角形, ∴ 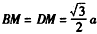 , ,∴ 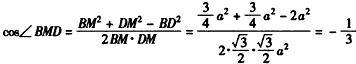 , ,∴二面角B-A′C-D的余弦值为  。 。 |
 |


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:高中数学 来源: 题型:
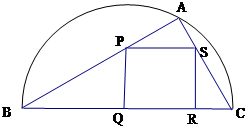 如图,某小区准备绿化一块直径为BC的半圆形空地,△ABC的内接正方形PQRS为一水池,△ABC外的地方种草,其余地方种花.若BC=a,∠ABC=θ,设△ABC的面积为S1,正方形PQRS的面积为S2,将比值
如图,某小区准备绿化一块直径为BC的半圆形空地,△ABC的内接正方形PQRS为一水池,△ABC外的地方种草,其余地方种花.若BC=a,∠ABC=θ,设△ABC的面积为S1,正方形PQRS的面积为S2,将比值| S1 | S2 |
查看答案和解析>>
科目:高中数学 来源: 题型:

查看答案和解析>>
科目:高中数学 来源: 题型:

查看答案和解析>>
科目:高中数学 来源:福建省厦门六中2011-2012学年高一下学期期中考试数学试题 题型:022
如图,将边长为1的正方形ABCD沿对角线AC折起,使得平面ADC⊥平面ABC,在折起后形成的三棱锥D-ABC中,给出下列三个命题:
①△DBC是等边三角形;
②AC⊥BD;
③三棱锥D-ABC的体积是![]() .
.

其中正确命题的序号是________.(写出所有正确命题的序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com