练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    投掷骰子2次，记第一次掷出的点数为a，第二次掷出的点数为b，现以（a，b）表示基本事件，事件“复数z1=a+bi与z2=1+2i对应的向量不共线”的对立事件的概率为    ．
    【答案】分析：事件“复数z1=a+bi与z2=1+2i对应的向量不共线”的对立事件为“复数z1=a+bi与z2=1+2i对应的向量共线”，从而可求a，b的关系，进而可求概率．
    解答：解：事件“复数z1=a+bi与z2=1+2i对应的向量不共线”的对立事件为“复数z1=a+bi与z2=1+2i对应的向量共线”，故b=2a，基本事件为（1，2），（2，4），（3，6），又所有基本事件共有36种，故所求的概率为，
    故答案为：
    点评：本题主要考查古典概型概率的求解，搞清基本事件的个数是解题的关键．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    把一颗骰子投掷两次，记第一次出现的点数为a2，第二次出现的点数为b2（其中a＞0，b＞0）．
    （Ⅰ）若记事件A“焦点在x轴上的椭圆的方程为
    x2
    a2
    +
    y2
    b2
    =1    ”，求事件A的概率；
    （Ⅱ）若记事件B“离心率为2的双曲线的方程为
    x2
    a2
    -
    y2
    b2
    =1    ”，求事件B的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    把一颗骰子投掷两次，记第一次出现的点数为a2，第二次出现的点数为b2（其中a＞0，b＞0）．试求：
    （Ⅰ）方程
    x2
    a2
    +
    y2
    b2
    =1    表示焦点在x轴上的椭圆的概率；
    （Ⅱ）方程
    x2
    a2
    -
    y2
    b2
    =1    表示离心率为2的双曲线的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    投掷骰子2次，记第一次掷出的点数为a，第二次掷出的点数为b，现以（a，b）表示基本事件，事件“复数z1=a+bi与z2=1+2i对应的向量不共线”的对立事件的概率为
     
    ．

    查看答案和解析>>

    科目：高中数学 来源：2011-2012年福建省四地六校高二第二次月考理科数学 题型：解答题

    (本题满分13分)

    把一颗骰子投掷两次，记第一次出现的点数为，第二次出现的点数为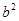（其中）．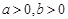

    （Ⅰ）若记事件“焦点在轴上的椭圆的方程为”，求事件的概率；

    （Ⅱ）若记事件“离心率为2的双曲线的方程为”，求事件的概率．

     

    查看答案和解析>>

    同步练习册答案