
【题目】函数![]() ,其中
,其中![]() ,
,![]() ,为实常数
,为实常数
(1)若![]() 时,讨论函数
时,讨论函数![]() 的单调性;
的单调性;
(2)若![]() 时,不等式
时,不等式![]() 在
在![]() 上恒成立,求实数
上恒成立,求实数![]() 的取值范围;
的取值范围;
(3)若![]() ,当
,当![]() 时,证明:
时,证明:![]() .
.
【答案】(1)见解析;(2) ![]() (3)见证明
(3)见证明
【解析】
(1)代入t的值,求得导函数,对a进行分类讨论,根据导数的正负确定单调区间即可.
(2)代入t的值,根据不等式分离参数,通过构造函数![]() ,再求
,再求![]() ,根据其单调性求得最大值即可得a的取值范围.
,根据其单调性求得最大值即可得a的取值范围.
(3)要证明不等式成立,根据分析法得到只需证明![]() 成立即可.通过构造函数
成立即可.通过构造函数![]() ,利用导数研究其单调性与最值,根据最小值即可得证.
,利用导数研究其单调性与最值,根据最小值即可得证.
解(1)定义域为![]() ,
,![]()
![]() ,
,
当![]() 时,
时,![]() ,
,![]()
![]() ,
,
![]() 在定义域
在定义域![]() 上单调递增;
上单调递增;
当![]() 时,
时,![]() 时,
时,![]() ,
,![]() 单调递增;
单调递增;
当![]() 时,
时,![]() .
.![]() 单调递减;
单调递减;
综上可知:当![]() 时,
时,![]() 的增区间为
的增区间为![]() ,无减区间;
,无减区间;
当![]() 时,增区间为
时,增区间为![]() ,减区间为
,减区间为![]() ;
;
(2)![]()
![]()
![]()
![]() 对任意
对任意![]() 恒成立.
恒成立.
即等价于![]() ,
,![]() ,
,
令![]() .
.
![]()
![]() ,
,![]() ,
,
![]() 在
在![]() 上单调递增,
上单调递增,
![]() ,
,
![]() .故
.故![]() 的取值范围为
的取值范围为![]() .
.
(3)要证明![]() ,即证明
,即证明![]() ,只要证
,只要证![]() ,
,
即证![]() ,只要证明
,只要证明![]() 即可,
即可,
令![]() ,
,![]() 在
在![]() 上是单调递增,
上是单调递增,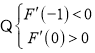 ,
,
![]() 在
在![]() 有唯一实根设为
有唯一实根设为![]() ,
,
且![]() ,
,
当![]() 时
时![]() ,
,![]() 单调递减
单调递减
当![]() 时,
时,![]() ,
,![]() 单调递增
单调递增
从而当![]() 时,
时,![]() 取得最小值,由
取得最小值,由![]() 得:
得:
![]() ,即
,即![]() ,
,
![]()
![]()
![]()
 ,
,
故当![]() 时,证得:
时,证得:![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如今我们的互联网生活日益丰富,除了可以很方便地网购,网络外卖也开始成为不少人日常生活中不可或缺的一部分![]() 市某调查机构针对该市市场占有率最高的两种网络外卖企业
市某调查机构针对该市市场占有率最高的两种网络外卖企业![]() 以下简称外卖A、外卖
以下简称外卖A、外卖![]() 的服务质量进行了调查,从使用过这两种外卖服务的市民中随机抽取了1000人,每人分别对这两家外卖企业评分,满分均为100分,并将分数分成5组,得到以下频数分布表:
的服务质量进行了调查,从使用过这两种外卖服务的市民中随机抽取了1000人,每人分别对这两家外卖企业评分,满分均为100分,并将分数分成5组,得到以下频数分布表:
分数 人数 种类 |
|
|
|
|
|
外卖A | 50 | 150 | 100 | 400 | 300 |
外卖B | 100 | 100 | 300 | 200 | 300 |
表中得分越高,说明市民对网络外卖服务越满意![]() 若得分不低于60分,则表明该市民对网络外卖服务质量评价较高
若得分不低于60分,则表明该市民对网络外卖服务质量评价较高![]() 现将分数按“服务质量指标”划分成以下四个档次:
现将分数按“服务质量指标”划分成以下四个档次:
分数 |
|
|
|
|
服务质量指标 | 0 | 1 | 2 | 3 |
视频率为概率,解决下列问题:
![]() 从该市使用过外卖A的市民中任选5人,记对外卖A服务质量评价较高的人数为X,求X的数学期望.
从该市使用过外卖A的市民中任选5人,记对外卖A服务质量评价较高的人数为X,求X的数学期望.
![]() 从参与调查的市民中随机抽取1人,试求其评分中外卖A的“服务质量指标”与外卖B的“服务质量指标”的差的绝对值等于2的概率;
从参与调查的市民中随机抽取1人,试求其评分中外卖A的“服务质量指标”与外卖B的“服务质量指标”的差的绝对值等于2的概率;
![]() 在M市工作的小王决定从外卖A、外卖B这两种网络外卖中选择一种长期使用,如果从这两种外卖的“服务质量指标”的期望角度看,他选择哪种外卖更合适?试说明理由.
在M市工作的小王决定从外卖A、外卖B这两种网络外卖中选择一种长期使用,如果从这两种外卖的“服务质量指标”的期望角度看,他选择哪种外卖更合适?试说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四棱锥![]() ,底面
,底面![]() 为菱形,
为菱形,![]() ,
,![]() 为
为![]() 上的点,过
上的点,过![]() 的平面分别交
的平面分别交![]() ,
,![]() 于点
于点![]() ,
,![]() ,且
,且![]() 平面
平面![]() .
.
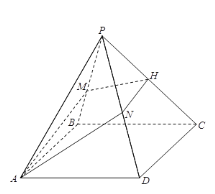
(1)证明:![]() ;
;
(2)当![]() 为
为![]() 的中点,
的中点,![]() ,
,![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,求
,求![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在四棱锥![]() 中,底面
中,底面![]() 是边长为
是边长为![]() 的正方形,
的正方形,![]() 是正三角形,CD平面PAD,E,F,G,O分别是PC,PD,BC,AD 的中点.
是正三角形,CD平面PAD,E,F,G,O分别是PC,PD,BC,AD 的中点.

(Ⅰ)求证:PO平面![]() ;
;
(Ⅱ)求平面EFG与平面![]() 所成锐二面角的大小;
所成锐二面角的大小;
(Ⅲ)线段![]() 上是否存在点
上是否存在点![]() ,使得直线
,使得直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,若存在,求线段
,若存在,求线段![]() 的长度;若不存在,说明理由.
的长度;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为提高城市居民生活幸福感,某城市公交公司大力确保公交车的准点率,减少居民乘车候车时间为此,该公司对某站台乘客的候车时间进行统计乘客候车时间受公交车准点率、交通拥堵情况、节假日人流量增大等情况影响在公交车准点率正常、交通拥堵情况正常、非节假日的情况下,乘客候车时间随机变量![]() 满足正态分布
满足正态分布![]() 在公交车准点率正常、交通拥堵情况正常、非节假日的情况下,调查了大量乘客的候车时间,经过统计得到如图频率分布直方图.
在公交车准点率正常、交通拥堵情况正常、非节假日的情况下,调查了大量乘客的候车时间,经过统计得到如图频率分布直方图.
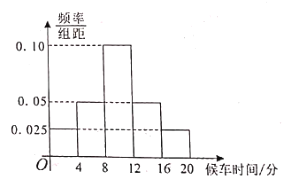
(1)在直方图各组中,以该组区间的中点值代表该组中的各个值,试估计![]() 的值;
的值;
(2)在统计学中,发生概率低于千分之三的事件叫小概率事件,一般认为,在正常情况下,一次试验中,小概率事件是不能发生的在交通拥堵情况正常、非节假日的某天,随机调查了该站的10名乘客的候车时间,发现其中有3名乘客候车时间超过15分钟,试判断该天公交车准点率是否正常,说明理由.
(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了让幼儿园大班的小朋友尝试以客体区分左手和右手,左肩和右肩,在游戏中提高细致戏察和辨别能力,同时能大胆地表达自己的想法,体验与同伴游戏的快乐,某位教师设计了一个名为(肩手左右)的游戏,方案如下:
游戏准备:
选取甲、乙两位小朋友面朝同一方向并排坐下进行游戏.教师站在两位小朋友面前出示游戏卡片.游戏卡片为两张白色纸板,一张纸板正反两面都打印有相同的”左“字,另一张纸板正反两面打印有相同的“右”字.
游戏进行:
一轮游戏(一轮游戏包含多次游戏直至决出胜者)开始后,教师站在参加游戏的甲、乙两位小朋友面前出示游戏卡片并大声报出出示的卡片上的“左”或者“右”字.两位小朋友如果听到“左”的指令,或者看到教师出示写有“左”字的卡片就应当将左手放至右肩上并大声喊出“停!”.小朋友如果听到“右”的指令,或者看到教师出示写有“右”字的卡片就应当将右手放至左肩上并大声喊出“停!”.最先完成指令动作的小朋友喊出“停!”时,两位小朋友都应当停止动作,教师根据两位小朋友的动作完成情况进行评分,至此游戏完成一次.
游戏评价:
为了方便描述问题,约定:对于每次游戏,若甲小朋友正确完成了指令动作且乙小朋友未完成则甲得1分,乙得﹣1分;若乙小朋友正确完成了指令动作且甲小朋友未完成则甲得﹣1分,乙得1分;若甲,乙两位小朋友都正确完成或都未正确完成指令动作,则两位小朋友均得0分.当两位小朋友中的一位比另外一位小朋友的分数多8分时,就停止本轮游戏,并判定得分高的小朋友获胜.现假设“甲小朋友能正确完成一次游戏中的指令动作的概率为α,乙小朋友能正确完成一次游戏中的指令动作的概率为β”,一次游戏中甲小朋友的得分记为X.
(1)求X的分布列;
(2)若甲小朋友、乙小朋友在一轮游戏开始时都赋予4分,pi(i=0,1,…,8)表示“甲小朋友的当前累计得分为i时,本轮游戏甲小朋友最终获胜”的概率,则P0=0,p8=1,pi=api﹣1+bpi+cpi+1(i=1,2,…,7),其中a=P(X=﹣1),b=P(X=0),c=P(X=1).假设α=0.5,β=0.8.
①证明:{pi+1﹣pi}(i=0,1,2,…,7)为等比数列;
②求p4,并根据p4的值说明这种游戏方案是否能够充分验证“甲小朋友能正确完成一次游戏中的指令动作的概率为0.5,乙小朋友能正确完成一次游戏中的指令动作的率为0.8”的假设.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com