
【题目】已知直线l与抛物线C:y2=4x交于A,B两点,M(2,y0)(y0≠0)为弦AB的中点,过M作AB的垂线交x轴于点P
(1)求点P的坐标;
(2)当弦AB最长时,求直线l的方程.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]()
【解析】
(1)设出直线方程,联立抛物线方程,由中点坐标即可得相关等式,求出AB的垂线,求其与![]() 轴的交点即可;
轴的交点即可;
(2)利用(1)中结论,求弦长的最值,求得当弦长最大时直线的方程即可.
(1)设直线方程为![]()
联立抛物线方程![]() ,
,
可得:![]()
当![]() 时,
时,
设![]()
故![]()
![]()
因为M(2,y0)为弦AB的中点
故![]() ,整理得:
,整理得:![]() ①
①
又点M(2,y0)在直线AB上,故![]() ②
②
故过M与AB垂直的直线方程为:
![]()
令![]() ,解得
,解得![]()
用①-②可得:![]()
因为![]() ,故
,故![]() ,则
,则![]()
即可得![]() ,
,
故与AB垂直的直线与![]() 轴的交点为
轴的交点为![]() .
.
(2)由弦长公式可得:
![]()
又因为![]() 解得
解得![]()
由①可知![]() ,代入上式得
,代入上式得![]()
故当且仅当![]() ,即
,即![]() ,
,![]() 时,弦长取得最大值;
时,弦长取得最大值;
此时直线方程为:![]()
整理即为:![]() 或
或![]() .
.
即弦长最大时,直线方程为:![]() 或
或![]() .
.


科目:高中数学 来源: 题型:
【题目】某工厂生产的产品中分正品与次品,正品重![]() ,次品重
,次品重![]() ,现有5袋产品(每袋装有10个产品),已知其中有且只有一袋次品(10个产品均为次品)如果将5袋产品以1~5编号,第
,现有5袋产品(每袋装有10个产品),已知其中有且只有一袋次品(10个产品均为次品)如果将5袋产品以1~5编号,第![]() 袋取出
袋取出![]() 个产品(
个产品(![]() ),并将取出的产品一起用秤(可以称出物体重量的工具)称出其重量
),并将取出的产品一起用秤(可以称出物体重量的工具)称出其重量![]() ,若次品所在的袋子的编号是2,此时的重量
,若次品所在的袋子的编号是2,此时的重量![]() _________
_________![]() ;若次品所在的袋子的编号是
;若次品所在的袋子的编号是![]() ,此时的重量
,此时的重量![]() _______
_______![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了减轻家庭困难的高中学生的经济负担,让更多的孩子接受良好的教育,国家施行高中生国家助学金政策,普通高中国家助学金平均资助标准为每生每年1500元,具体标准由各地结合实际在1000元至3000元范围内确定,可以分为两或三档.各学校积极响应政府号召,通过各种形式宣传国家助学金政策.为了解某高中学校对国家助学金政策的宣传情况,拟采用随机抽样的方法抽取部分学生进行采访调查.
(1)若该高中学校有2000名在校学生,编号分别为0001,0002,0003,…,2000,请用系统抽样的方法,设计一个从这2000名学生中抽取50名学生的方案.(写出必要的步骤)
(2)该校根据助学金政策将助学金分为3档,1档每年3000元,2档每年2000元,3档每年1000元,某班级共评定出3个1档,2个2档,1个3档,若从该班获得助学金的学生中选出2名写感想,求这2名同学不在同一档的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正三棱柱ABC-A1B1C1中,AB=AA1=2,点P,Q分别为A1B1,BC的中点.
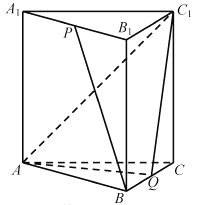
(1)求异面直线BP与AC1所成角的余弦值;
(2)求直线CC1与平面AQC1所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() ,线段
,线段![]() 、
、![]() 都是圆
都是圆![]() 的弦,且
的弦,且![]() 与
与![]() 垂直且相交于坐标原点
垂直且相交于坐标原点![]() ,如图所示,设△
,如图所示,设△![]() 的面积为
的面积为![]() ,设△
,设△![]() 的面积为
的面积为![]() .
.
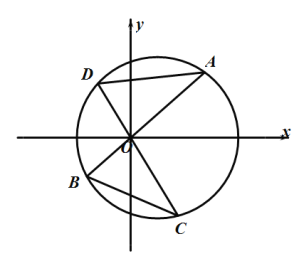
(1)设点![]() 的横坐标为
的横坐标为![]() ,用
,用![]() 表示
表示![]() ;
;
(2)求证:![]() 为定值;
为定值;
(3)用![]() 、
、![]() 、
、![]() 、
、![]() 表示出
表示出![]() ,试研究
,试研究![]() 是否有最小值,如果有,求出最小值,并写出此时直线
是否有最小值,如果有,求出最小值,并写出此时直线![]() 的方程;若没有最小值,请说明理由.
的方程;若没有最小值,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三棱锥![]() 的棱长均为6,其内有
的棱长均为6,其内有![]() 个小球,球
个小球,球![]() 与三棱锥
与三棱锥![]() 的四个面都相切,球
的四个面都相切,球![]() 与三棱锥
与三棱锥![]() 的三个面和球
的三个面和球![]() 都相切,如此类推,…,球
都相切,如此类推,…,球![]() 与三棱锥
与三棱锥![]() 的三个面和球
的三个面和球![]() 都相切(
都相切(![]() ,且
,且![]() ),则球
),则球![]() 的体积等于__________,球
的体积等于__________,球![]() 的表面积等于__________.
的表面积等于__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平行六面体ABCD-A1B1C1D1中,AA1⊥平面ABCD,且AB=AD=2,AA1=![]() ,∠BAD=120°.
,∠BAD=120°.
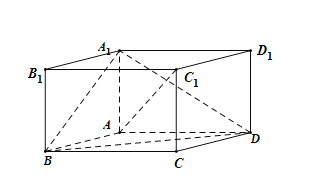
(1)求异面直线A1B与AC1所成角的余弦值;
(2)求二面角B-A1D-A的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() (
(![]() )的两焦点与短轴两端点围成面积为12的正方形.
)的两焦点与短轴两端点围成面积为12的正方形.
(1)求椭圆C的标准方程;
(2)我们称圆心在椭圆上运动,半径为![]() 的圆是椭圆的“卫星圆”.过原点O作椭圆C的“卫星圆”的两条切线,分别交椭圆C于A、B两点,若直线
的圆是椭圆的“卫星圆”.过原点O作椭圆C的“卫星圆”的两条切线,分别交椭圆C于A、B两点,若直线![]() 、
、![]() 的斜率为
的斜率为![]() 、
、![]() ,当
,当![]() 时,求此时“卫星圆”的个数.
时,求此时“卫星圆”的个数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com