
【题目】以直角坐标系的原点O为极点,x轴的正半轴为极轴建立极坐标系.
(1)将直线l:  (t为参数)化为极坐标方程;
(t为参数)化为极坐标方程;
(2)设P是(1)中直线l上的动点,定点A( ![]() ,
, ![]() ),B是曲线ρ=﹣2sinθ上的动点,求|PA|+|PB|的最小值.
),B是曲线ρ=﹣2sinθ上的动点,求|PA|+|PB|的最小值.
【答案】
(1)解:由直线l: 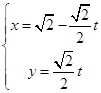 (t为参数)消去参数t,可得x+y=
(t为参数)消去参数t,可得x+y= ![]() ,化为极坐标方程ρcosθ+ρsinθ=
,化为极坐标方程ρcosθ+ρsinθ= ![]()
(2)解:定点A( ![]() ,
, ![]() ),化为A(1,1).
),化为A(1,1).
曲线ρ=﹣2sinθ化为ρ2=﹣2ρsinθ,∴直角坐标方程为:x2+y2=﹣2y,
配方为x2+(y+1)2=1.
可得圆心C(0,﹣1).
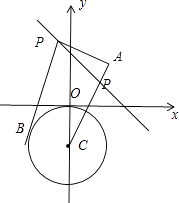
连接AC交直线l于点P,交⊙C于点B,
|AC|= ![]() =
= ![]() ,
,
∴|PA|+|PB|的最小值=|AC|﹣r= ![]() ﹣1.
﹣1.
【解析】(1)由直线l: 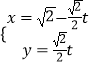 (t为参数)消去参数t,可得x+y=
(t为参数)消去参数t,可得x+y= ![]() ,利用
,利用 ![]() 即可化为极坐标方程;(2)定点A(
即可化为极坐标方程;(2)定点A( ![]() ,
, ![]() ),化为A(1,1).曲线ρ=﹣2sinθ化为ρ2=﹣2ρsinθ,可得直角坐标方程:x2+(y+1)2=1.可得圆心C(0,﹣1).连接AC交直线l于点P,交⊙C于点B,可得|PA|+|PB|的最小值=|AC|﹣r.
),化为A(1,1).曲线ρ=﹣2sinθ化为ρ2=﹣2ρsinθ,可得直角坐标方程:x2+(y+1)2=1.可得圆心C(0,﹣1).连接AC交直线l于点P,交⊙C于点B,可得|PA|+|PB|的最小值=|AC|﹣r.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知右焦点为F(c,0)的椭圆M: ![]() =1(a>b>0)过点
=1(a>b>0)过点 ![]() ,且椭圆M关于直线x=c对称的图形过坐标原点.
,且椭圆M关于直线x=c对称的图形过坐标原点.
(1)求椭圆M的方程;
(2)过点(4,0)且不垂直于y轴的直线与椭圆M交于P,Q两点,点Q关于x轴的对称原点为E,证明:直线PE与x轴的交点为F.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a>0,函数f(x)=ax2+bx+c,若x0满足关于x的方程2ax+b=0,则下列选项的命题中为假命题的是( )
A.x∈R,f(x)≤f(x0)
B.x∈R,f(x)≥f(x0)
C.x∈R,f(x)≤f(x0)
D.x∈R,f(x)≥f(x0)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场出售两款型号不同的手机,由于市场需求发生变化,第一款手机连续两次提价10%,第二款手机连续两次降价10%,结果都以1210元出售.
(1)求第一款手机的原价;
(2)若该商场同时出售两款手机各一部,求总售价与总原价之间的差额.(结果精确到整数)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设等差数列{an}满足(1﹣a1008)5+2016(1﹣a1008)=1,(1﹣a1009)5+2016(1﹣a1009)=﹣1,数列{an}的前n项和记为Sn , 则( )
A.S2016=2016,a1008>a1009
B.S2016=﹣2016,a1008>a1009
C.S2016=2016,a1008<a1009
D.S2016=﹣2016,a1008<a1009
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,直线C1的参数方程为 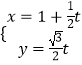 (t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ2(1+2sin2θ)=3.
(t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ2(1+2sin2θ)=3.
(Ⅰ)写出C1的普通方程和C2的直角坐标方程;
(Ⅱ)直线C1与曲线C2相交于A,B两点,点M(1,0),求||MA|﹣|MB||.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,函数
,函数![]() .
.
(1)若函数![]() ,
, ![]() 的最小值为-16,求实数
的最小值为-16,求实数![]() 的值;
的值;
(2)若函数![]() 在区间
在区间![]() 上是单调减函数,求实数
上是单调减函数,求实数![]() 的取值范围;
的取值范围;
(3)当![]() 时,不等式
时,不等式![]() 的解集为
的解集为![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com