
已知 的图象关于坐标原点对称。
的图象关于坐标原点对称。
(1)求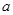 的值,并求出函数
的值,并求出函数 的零点;
的零点;
(2)若函数 在[0,1]内存在零点,求实数b的取值范围;
在[0,1]内存在零点,求实数b的取值范围;
(3)设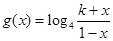 ,已知
,已知 的反函数
的反函数 =
= ,若不等式
,若不等式 在
在 上恒成立,求满足条件的最小整数k的值。
上恒成立,求满足条件的最小整数k的值。
(1)F(x)的零点为x=1;(2)2≤b≤7;(3)满足条件的最小整数k的值是8
解析试题分析:(1)根据函数的图象关于原点对称,可得f(x)是定义在R的奇函数,图象必过原点,即f(0)=0,求出a的值,求出函数F(x)的解析式,解指数方程求求出函数的零点;
(2)函数 在[0,1]内存在零点,方程(2x)2+2x+1-1-b=0在[0,1]内有解,分析函数b=(2x)2+2x+1-1在[0,1]内的单调性,及端点的函数值符号,进而根据零点存在定理得到结论;
在[0,1]内存在零点,方程(2x)2+2x+1-1-b=0在[0,1]内有解,分析函数b=(2x)2+2x+1-1在[0,1]内的单调性,及端点的函数值符号,进而根据零点存在定理得到结论;
(3)由不等式f-1(x)≤g(x)在 上恒成立,利用基本不等式可求出满足条件的k的范围,进而求出最小整数k的值.
上恒成立,利用基本不等式可求出满足条件的k的范围,进而求出最小整数k的值.
试题解析:(1)由题意知f(x)是R上的奇函数,

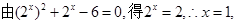
即F(x)的零点为x="1." 4分
(2)
由题设知h(x)=0在[0,1]内有解,


 在[0,1]内存在零点 8分
在[0,1]内存在零点 8分
(3)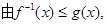
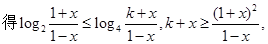
显然

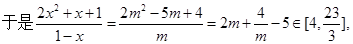
 14分
14分
考点:函数的性质的综合应用.


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案科目:高中数学 来源: 题型:解答题
已知中心在原点,焦点在 轴上的椭圆
轴上的椭圆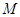 的离心率为
的离心率为 ,椭圆上异于长轴顶点的任意点
,椭圆上异于长轴顶点的任意点 与左右两焦点
与左右两焦点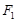 、
、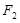 构成的三角形中面积的最大值为
构成的三角形中面积的最大值为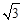 .
.
(1)求椭圆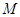 的标准方程;
的标准方程;
(2)已知点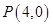 ,连接
,连接 与椭圆的另一交点记为
与椭圆的另一交点记为 ,若
,若 与椭圆相切时
与椭圆相切时 、
、 不重合,连接
不重合,连接 与椭圆的另一交点记为
与椭圆的另一交点记为 ,求
,求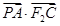 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某市2013年发放汽车牌照12万张,其中燃油型汽车牌照10万张,电动型汽车2万张.为了节能减排和控制总量,从2013年开始,每年电动型汽车牌照按50%增长,而燃油型汽车牌照每一年比上一年减少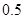 万张,同时规定一旦某年发放的牌照超过15万张,以后每一年发放的电动车的牌照的数量维持在这一年的水平不变.
万张,同时规定一旦某年发放的牌照超过15万张,以后每一年发放的电动车的牌照的数量维持在这一年的水平不变.
(1)记2013年为第一年,每年发放的燃油型汽车牌照数构成数列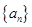 ,每年发放的电动型汽车牌照数为构成数列
,每年发放的电动型汽车牌照数为构成数列 ,完成下列表格,并写出这两个数列的通项公式;
,完成下列表格,并写出这两个数列的通项公式;
(2)从2013年算起,求二十年发放的汽车牌照总量.
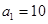 | 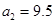 | 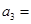 | 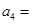 | |
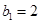 |  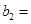 3 3 | 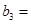 | 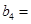 | |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某校要建一个面积为450平方米的矩形球场,要求球场的一面利用旧墙,其他各面用钢筋网围成,且在矩形一边的钢筋网的正中间要留一个3米的进出口(如图).设矩形的长为 米,钢筋网的总长度为
米,钢筋网的总长度为 米.
米.
(1)列出 与
与 的函数关系式,并写出其定义域;
的函数关系式,并写出其定义域;
(2)问矩形的长与宽各为多少米时,所用的钢筋网的总长度最小?
(3)若由于地形限制,该球场的长和宽都不能超过25米,问矩形的长与宽各为多少米时,所用的钢筋网的总长度最小?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图所示,为了制作一个圆柱形灯笼,先要制作4个全等的矩形骨架,总计耗用9.6米铁丝,再用S平方米塑料片制成圆柱的侧面和下底面(不安装上底面).当圆柱底面半径r取何值时,S取得最大值?并求出该最大值(结果精确到0.01平方米).
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数f(x)=log4(4x+1)+kx(k∈R)是偶函数.
(1)求k的值;
(2)设g(x)=log4 ,若函数f(x)与g(x)的图象有且只有一个公共点,求实数a的取值范围.
,若函数f(x)与g(x)的图象有且只有一个公共点,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com