
【题目】如图在四面体![]() 中,
中,![]() 是边长为2的等边三角形,
是边长为2的等边三角形,![]() 为直角三角形,其中
为直角三角形,其中![]() 为直角顶点,
为直角顶点,![]() .
.![]() 分别是线段
分别是线段![]() 上的动点,且四边形
上的动点,且四边形![]() 为平行四边形.
为平行四边形.

(1)求证:![]() 平面
平面![]() ,
,![]() 平面
平面![]() ;
;
(2)试探究当二面角![]() 从0°增加到90°的过程中,线段
从0°增加到90°的过程中,线段![]() 在平面
在平面![]() 上的投影所扫过的平面区域的面积;
上的投影所扫过的平面区域的面积;
(3)设![]()
![]() ,且
,且![]() 为等腰三角形,当
为等腰三角形,当![]() 为何值时,多面体
为何值时,多面体![]() 的体积恰好为
的体积恰好为![]() ?
?
【答案】(1)见解析 (2)![]() (3)
(3)![]()
【解析】
(1)先通过线面平行的判定定理,证得![]() 平面
平面![]() ,通过线面平行的性质定理,证得
,通过线面平行的性质定理,证得![]() ,由此证得
,由此证得![]() 平面
平面![]() ;同理证得
;同理证得![]() 平面
平面![]() .
.
(2)画出![]() 为
为![]() 、
、![]() 时
时![]() 的投影,由此判断出线段
的投影,由此判断出线段![]() 在平面
在平面![]() 上的投影所扫过的平面区域,进而求得区域的面积.
上的投影所扫过的平面区域,进而求得区域的面积.
(3)先求得三棱锥![]() 的面积为
的面积为![]() ,通过分割的方法,得到
,通过分割的方法,得到![]() ,分别求得
,分别求得![]() 与
与![]() 的关系式,再由
的关系式,再由![]() 列方程,解方程求得
列方程,解方程求得![]() 的值.
的值.
(1)∵四边形![]() 为平行四边形,
为平行四边形,
∴![]() .而
.而![]() 面
面![]() ,
,![]() 面
面![]() ,
,
∴![]() 面
面![]() .而
.而![]() 面
面![]() ,面
,面![]() 面
面![]() ,
,
∴![]() ∥
∥![]() .而
.而![]() 面
面![]() ,
,![]() 面
面![]() ,
,
∴![]() ∥平面
∥平面![]() .同理,
.同理,![]() ∥平面
∥平面![]() ;
;
(2)∵![]() ,
,
∴![]() 在平面
在平面![]() 上的投影满足
上的投影满足![]() ,即
,即![]() 在线段
在线段![]() 的中垂线上.
的中垂线上.
如图所示,将![]() 补成边长为
补成边长为![]() 的正
的正![]() ,
,
当二面角![]() 为
为![]() 角时,即点
角时,即点![]() 在平面
在平面![]() 上,此时
上,此时![]() 为
为![]() ,
,
当二面角![]() 为
为![]() 角时,此时
角时,此时![]() 为
为![]() 中点
中点![]() ,
,
故![]() 在平面
在平面![]() 上的投影所扫过的平面区域为
上的投影所扫过的平面区域为![]() ,而
,而![]() ,
,
故线段![]() 在平面
在平面![]() 上的投影所扫过的平面区域的面积为
上的投影所扫过的平面区域的面积为![]() ;
;

(3)∵![]() ,
,![]() ,且
,且![]() 为等腰三角形,∴
为等腰三角形,∴![]() .
.
取![]() 中点
中点![]() ,易得:
,易得:![]() ,
,![]() ,
,![]() ,
,
满足:![]() ,根据勾股定理可知
,根据勾股定理可知![]() .
.
∴![]() 平面
平面![]() .∴
.∴![]() .
.
而多面体![]() 的体积恰好为
的体积恰好为![]() ,即多面体
,即多面体![]() 的体积恰为四面体
的体积恰为四面体![]() 体积的一半.
体积的一半.
连接![]() .
.
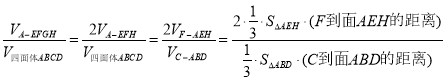
![]() ,∴
,∴![]() .
.

![]() ,∴
,∴![]() .
.
∴![]() ,
,
∴![]() ,整理:
,整理:![]() ,即
,即![]() ,
,
解得:![]() (
(![]() 舍去).
舍去).


科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,椭圆C:![]() 的右准线方程为x=2,且两焦点与短轴的一个顶点构成等腰直角三角形.
的右准线方程为x=2,且两焦点与短轴的一个顶点构成等腰直角三角形.
(1)求椭圆C的方程;
(2)假设直线l:![]() 与椭圆C交于A,B两点.①若A为椭圆的上顶点,M为线段AB中点,连接OM并延长交椭圆C于N,并且
与椭圆C交于A,B两点.①若A为椭圆的上顶点,M为线段AB中点,连接OM并延长交椭圆C于N,并且![]() ,求OB的长;②若原点O到直线l的距离为1,并且
,求OB的长;②若原点O到直线l的距离为1,并且![]() ,当
,当![]() 时,求△OAB的面积S的范围.
时,求△OAB的面积S的范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数![]() 图象上所有点的横坐标缩短为原来的
图象上所有点的横坐标缩短为原来的![]() ,纵坐标不变,再向右平移
,纵坐标不变,再向右平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象,则下列说法正确的是( )
的图象,则下列说法正确的是( )
A. 函数![]() 的一条对称轴是
的一条对称轴是![]()
B. 函数![]() 的一个对称中心是
的一个对称中心是![]()
C. 函数![]() 的一条对称轴是
的一条对称轴是![]()
D. 函数![]() 的一个对称中心是
的一个对称中心是![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】曾玉、刘云、李梦、张熙四人被北京大学、清华大学、武汉大学和复旦大学录取,他们分别被哪个学校录取,同学们做了如下的猜想
甲同学猜:曾玉被武汉大学录取,李梦被复旦大学录取
同学乙猜:刘云被清华大学录取,张熙被北京大学录取
同学丙猜:曾玉被复旦大学录取,李梦被清华大学录取
同学丁猜:刘云被清华大学录取,张熙被武汉大学录取
结果,恰好有三位同学的猜想各对了一半,还有一位同学的猜想都不对
那么曾玉、刘云、李梦、张熙四人被录取的大小可能是( )
A.北京大学、清华大学、复旦大学、武汉大学
B.武汉大学、清华大学、复旦大学、北京大学
C.清华大学、北京大学、武汉大学 、复旦大学
D.武汉大学、复旦大学、清华大学、北京大学
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列命题:
①命题“若![]() ,则方程
,则方程![]() 无实根”的否命题;
无实根”的否命题;
②命题“在![]() 中,
中,![]() ,那么
,那么![]() 为等边三角形”的逆命题;
为等边三角形”的逆命题;
③命题“若![]() ,则
,则![]() ”的逆否命题;
”的逆否命题;
④“若![]() ,则
,则![]() 的解集为
的解集为![]() ”的逆命题;
”的逆命题;
其中真命题的序号为( )
A.①②③④B.①②④C.②④D.①②③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() ,
,![]() ,给定下列命题:
,给定下列命题:
①若方程![]() 有两个不同的实数根,则
有两个不同的实数根,则![]() ;
;
②若方程![]() 恰好只有一个实数根,则
恰好只有一个实数根,则![]() ;
;
③若![]() ,总有
,总有![]() 恒成立,则
恒成立,则![]() ;
;
④若函数![]() 有两个极值点,则实数
有两个极值点,则实数![]() .
.
则正确命题的个数为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C经过点![]() ,
,![]() 两点,且圆心C在直线
两点,且圆心C在直线![]() 上.
上.
(1)求圆C的方程;
(2)设![]() ,对圆C上任意一点P,在直线MC上是否存在与点M不重合的点N,使
,对圆C上任意一点P,在直线MC上是否存在与点M不重合的点N,使![]() 是常数,若存在,求出点N坐标;若不存在,说明理由.
是常数,若存在,求出点N坐标;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com