
【题目】已知函数![]() ,
, ![]() .
.
(1)求函数![]() 的单调递增区间;
的单调递增区间;
(2)若![]() ,
, ![]() ,且
,且![]() ,
, ![]() ,
, ![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
【答案】(1) 函数![]() 的单调递增区间为
的单调递增区间为![]() ;(2)
;(2) ![]() .
.
【解析】试题分析:(1)![]() , 解得
, 解得![]() ,从而得到增区间;(2)
,从而得到增区间;(2)![]() ,
, ![]() ,
, ![]() 等价于
等价于![]() 对
对![]() 恒成立,或
恒成立,或![]() 对
对![]() 恒成立,而
恒成立,而![]() ,只需研究
,只需研究![]() 的符号情况即可.
的符号情况即可.
试题解析:
(1)依题意, ![]() ,
,
令![]() ,解得
,解得![]() ,故函数
,故函数![]() 的单调递增区间为
的单调递增区间为![]() .
.
(2)当![]() ,对任意的
,对任意的![]() ,都有
,都有![]() ;
;
当![]() 时,对任意的
时,对任意的![]() ,都有
,都有![]() ;
;
故![]() 对
对![]() 恒成立,或
恒成立,或![]() 对
对![]() 恒成立,
恒成立,
而![]() ,设函数
,设函数![]() ,
, ![]() .
.
则![]() 对
对![]() 恒成立,或
恒成立,或![]() 对
对![]() 恒成立,
恒成立, ![]() ,
,
①当![]() 时,∵
时,∵![]() ,∴
,∴![]() ,∴
,∴![]() 恒成立,
恒成立,
∴![]() 在
在![]() 上单调递增,
上单调递增, ![]() ,
,
故![]() 在
在![]() 上恒成立,符合题意.
上恒成立,符合题意.
②当![]() 时,令
时,令![]() ,得
,得![]() ,令
,令![]() ,得
,得![]() ,
,
故![]() 在
在![]() 上单调递减,所以
上单调递减,所以![]() ,
,
而![]() ,设函数
,设函数![]() ,
, ![]() ,
,
则![]() ,令
,令![]() ,则
,则![]() (
(![]() )恒成立,
)恒成立,
∴![]() 在
在![]() 上单调递增,∴
上单调递增,∴![]() 恒成立,
恒成立,
∴![]() 在
在![]() 上单调递增,∴
上单调递增,∴![]()
![]() 恒成立,
恒成立,
即![]() ,而
,而![]() ,不合题意.
,不合题意.
综上,故实数![]() 的取值范围为
的取值范围为![]() .
.


科目:高中数学 来源: 题型:
【题目】
已知动圆![]() 恒过
恒过![]() 且与直线
且与直线![]() 相切,动圆圆心
相切,动圆圆心![]() 的轨迹记为
的轨迹记为![]() ;直线
;直线![]() 与
与![]() 轴的交点为
轴的交点为![]() ,过点
,过点![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 与轨迹
与轨迹![]() 有两个不同的公共点
有两个不同的公共点![]() ,
, ![]() ,
, ![]() 为坐标原点.
为坐标原点.
(1)求动圆圆心![]() 的轨迹
的轨迹![]() 的方程,并求直线
的方程,并求直线![]() 的斜率
的斜率![]() 的取值范围;
的取值范围;
(2)点![]() 是轨迹
是轨迹![]() 上异于
上异于![]() ,
, ![]() 的任意一点,直线
的任意一点,直线![]() ,
, ![]() 分别与过
分别与过![]() 且垂直于
且垂直于![]() 轴的直线交于
轴的直线交于![]() ,
, ![]() ,证明:
,证明: ![]() 为定值,并求出该定值;
为定值,并求出该定值;
(3)对于(2)给出一般结论:若点![]() ,直线
,直线![]() ,其它条件不变,求
,其它条件不变,求![]() 的值(可以直接写出结果).
的值(可以直接写出结果).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列四个命题:
①由样本数据得到的回归方程 ![]() 必过样本点的中心(
必过样本点的中心( ![]() ,
, ![]() );
);
②用相关指数R2来刻画回归效果,R2的值越小,说明模型的拟合效果越好;
③若线性回归方程为 ![]() =3﹣2.5x,则变量x每增加1个单位时,y平均减少2.5个单位;
=3﹣2.5x,则变量x每增加1个单位时,y平均减少2.5个单位;
④在残差图中,残差点分布的带状区域的宽度越窄,残差平方和越小.
上述四个命题中,正确命题的个数为( )
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场每天以每件100元的价格购入A商品若干件,并以每件200元的价格出售,若所购进的A商品前8小时没有售完,则商场对没卖出的A商品以每件60元的低价当天处理完毕(假定A商品当天能够处理完).该商场统计了100天A商品在每天的前8小时的销售量,制成如表格.
前8小时的销售量t(单位:件) | 5 | 6 | 7 |
频 数 | 40 | 35 | 25 |
(1)若某天该商场共购入7件A商品,在前8个小时售出5件. 若这些产品被7名不同的顾客购买,现从这7名顾客中随机选3人进行回访,记X表示这3人中以每件200元的价格购买的人数,求X的分布列;
(2)将频率视为概率,要使商场每天购进A商品时所获得的平均利润最大,则每天应购进几件A商品,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】抽样调查某大型机器设备使用年限x和该年支出维修费用y(万元),得到数据如表
使用年限x | 2 | 3 | 4 | 5 | 6 |
维修费用y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
部分数据分析如下 ![]() =25,
=25, ![]() yi=112.3,
yi=112.3, ![]() =90
=90
参考公式:线性回归直线方程为 ![]() ,
, 
(1)求线性回归方程;
(2)由(1)中结论预测第10年所支出的维修费用.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】未来制造业对零件的精度要求越来越高. ![]() 打印通常是采用数字技术材料打印机来实现的,常在模具 制造、工业设计等领域被用于制造模型,后逐渐用于一些产品的直接制造,已经有使用这种技术打印而成的零部件.该技术应用十分广泛,可以预计在未来会有广阔的发展空间.某制造企业向
打印通常是采用数字技术材料打印机来实现的,常在模具 制造、工业设计等领域被用于制造模型,后逐渐用于一些产品的直接制造,已经有使用这种技术打印而成的零部件.该技术应用十分广泛,可以预计在未来会有广阔的发展空间.某制造企业向![]() 高校
高校![]() 打印实验团队租用一台
打印实验团队租用一台![]() 打印设备,用于打印一批对内径有较高精度要求的零件.该团队在实验室打印出了一批这样的零件,从中随机抽取10件零件,度量其内径的茎叶图如图所示(单位:
打印设备,用于打印一批对内径有较高精度要求的零件.该团队在实验室打印出了一批这样的零件,从中随机抽取10件零件,度量其内径的茎叶图如图所示(单位: ![]() ).
).
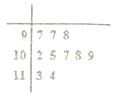
(1)计算平均值![]() 与标准差
与标准差![]() ;
;
(2)假设这台![]() 打印设备打印出品的零件内径
打印设备打印出品的零件内径![]() 服从正态分布
服从正态分布![]() ,在抽检零件中,如果出现了尺寸在
,在抽检零件中,如果出现了尺寸在![]() 之外的零件,就认为打印过程可能出现了异常情况,需对打印设备进行检查再调试.该团队到工厂安装调试后,试打了5个零件.度量其内径分别为(单位:
之外的零件,就认为打印过程可能出现了异常情况,需对打印设备进行检查再调试.该团队到工厂安装调试后,试打了5个零件.度量其内径分别为(单位: ![]() ): 86、95、103、109、118,试问此打印设备是否需要进一步调试,为什么?
): 86、95、103、109、118,试问此打印设备是否需要进一步调试,为什么?
参考数据: ![]() ,
, ![]() ,
,
![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】天水市第一次联考后,某校对甲、乙两个文科班的数学考试成绩进行分析,
规定:大于或等于120分为优秀,120分以下为非优秀.统计成绩后,
得到如下的![]() 列联表,且已知在甲、乙两个文科班全部110人中随机抽取1人为优秀的概率为
列联表,且已知在甲、乙两个文科班全部110人中随机抽取1人为优秀的概率为![]() .
.
优秀 | 非优秀 | 合计 | |
甲班 | 10 | ||
乙班 | 30 | ||
合计 | 110 |
(1)请完成上面的列联表;
(2)根据列联表的数据,若按99.9%的可靠性要求,能否认为“成绩与班级有关系”;
(3)若按下面的方法从甲班优秀的学生中抽取一人:把甲班优秀的10名学生从2到11进行编号,先后两次抛掷一枚均匀的骰子,出现的点数之和为被抽取人的序号。试求抽到9号或10号的概率。
参考公式与临界值表:![]() 。
。
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC的顶点A(0,1),AB边上的中线CD所在的直线方程为2x﹣2y﹣1=0,AC边上的高BH所在直线的方程为y=0.
(1)求△ABC的顶点B、C的坐标;
(2)若圆M经过不同的三点A、B、P(m,0),且斜率为1的直线与圆M相切于点P,求圆M的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com