
已知直三棱柱![]() 中,△
中,△![]() 为等腰直角三角形,∠
为等腰直角三角形,∠![]() =90°,且
=90°,且![]() =
=![]() ,
,![]() 、
、![]() 、
、![]() 分别为
分别为![]() 、
、![]() 、
、![]() 的中点.
的中点.
⑴求异面直线![]() 与
与![]() 的夹角余弦值;
的夹角余弦值;
⑵求证:![]() ∥平面
∥平面![]() ;
;
⑶求证:![]() ⊥平面
⊥平面![]() .
.
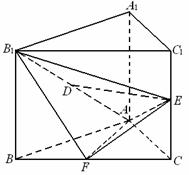
解:(1)做FH//AC, cos∠B1FH即所求,Rt△B1FH中,cos∠B1FH=![]()
(2)方法i:设G是AB的中点,连结DG,
则DG平行且等于EC,
所以四边形DECG是平行四边形,所以DE//GC,
从而DE∥平面ABC.
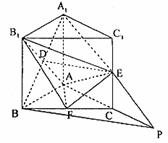
方法ii:连接A1B、A1E,并延长A1E交AC的延长线
于点P,连接BP.由E为C1C的中点,A1C1∥CP,
可证A1E=EP,
∵D、E是A1B、A1P的中点,∴DE∥BP,
又∵BP![]() 平面ABC,DE
平面ABC,DE![]() 平面ABC,∴DE∥平面ABC
平面ABC,∴DE∥平面ABC
(3)∵△ABC为等腰直角三角形,F为BC的中点,
∴BC⊥AF,又∵B1B⊥平面ABC,可证B1F⊥AF,
设![]() =
=![]() ,则
,则![]()
∴B1F⊥EF,∴![]() ⊥平面
⊥平面![]() ;
;


 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:高中数学 来源: 题型:
(本小题满分14分)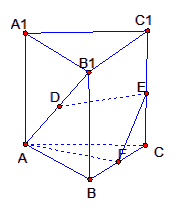 已知直三棱柱
已知直三棱柱![]() 中,
中,![]() 为等腰直角三角形,
为等腰直角三角形,![]() ,且
,且![]() ,
,![]() 分别为
分别为![]() 的中点,
的中点,
(1)求证:![]() //平面
//平面![]() ;
;
(2)求证:![]() 平面
平面![]() ;
;
(3)求三棱锥E-AB![]() F的体积。
F的体积。
查看答案和解析>>
科目:高中数学 来源:2012-2013学年辽宁沈阳二中等重点中学协作体高三领航高考预测(六)文数学卷(解析版) 题型:解答题
(本小题满分12分)已知直三棱柱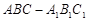 中,△
中,△ 为等腰直角三角形,∠
为等腰直角三角形,∠ =
= ,且
,且 =
=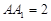 ,
, 、
、 、
、 分别为
分别为 、
、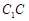 、
、 的中点.
的中点.
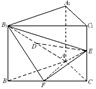
(1)求证: ∥平面
∥平面 ;
;
(2)求证: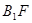 ⊥平面
⊥平面 ;
;
(3)求三棱锥 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源:2014届福建省等五校高一第一学期期末联考数学 题型:解答题
(本小题满分12分)已知直三棱柱 中,
中, ,
, 为
为 中点,
中点, 为
为 中点,侧面
中点,侧面 为正方形。
为正方形。
(1)证明: 平面
平面 ;
;
(2)证明: ;
;

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com