
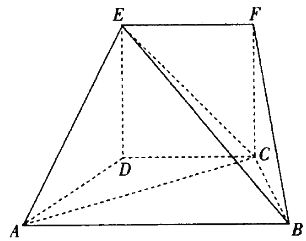
【题目】在如图所示的几何体中,四边形CDEF为正方形,四边形ABCD为梯形,![]() ,
,![]() ,
,![]() ,
,![]() 平面ABCD.
平面ABCD.
![]() 求BE与平面EAC所成角的正弦值;
求BE与平面EAC所成角的正弦值;
![]() 线段BE上是否存在点M,使平面
线段BE上是否存在点M,使平面![]() 平面DFM?若存在,求
平面DFM?若存在,求![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】(1)![]() ;(2)见解析
;(2)见解析
【解析】
![]() 以C为原点,CD为x轴,CB为y轴,CF为z轴,建立空间直角坐标系,求出平面EAC的法向量,利用向量法能求出BE与平面EAC所成角的正弦值.
以C为原点,CD为x轴,CB为y轴,CF为z轴,建立空间直角坐标系,求出平面EAC的法向量,利用向量法能求出BE与平面EAC所成角的正弦值.
![]() 设线段BE上存在点
设线段BE上存在点![]() b,
b,![]() ,
,![]() ,
,![]() ,使平面
,使平面![]() 平面DFM,求出平面DMF的法向量和平面EAC的法向量,利用向量法求出线段BE上不存在点M,使平面
平面DFM,求出平面DMF的法向量和平面EAC的法向量,利用向量法求出线段BE上不存在点M,使平面![]() 平面DFM.
平面DFM.
![]() 四边形CDEF为正方形,四边形ABCD为梯形,
四边形CDEF为正方形,四边形ABCD为梯形,![]() ,
,![]() ,
,![]() 平面ABCD.
平面ABCD.
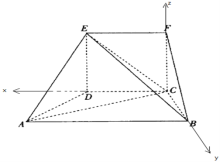
![]() 以C为原点,CD为x轴,CB为y轴,
以C为原点,CD为x轴,CB为y轴,
CF为z轴,建立空间直角坐标系,
设![]() ,则
,则![]() 1,
1,![]() ,
,
![]() 0,
0,![]() ,
,![]() 1,
1,![]() ,
,
![]() 0,
0,![]() ,
,![]() 0,
0,![]() ,
,
![]() ,
,![]() 1,
1,![]() ,
,
![]() 0,
0,![]() ,
,
设平面EAC的法向量![]() y,
y,![]() ,
,
则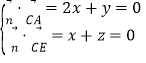 ,取
,取![]() ,
,
得![]() ,
,
设BE与平面EAC所成角为![]() ,
,
则![]() .
.
![]() 与平面EAC所成角的正弦值为
与平面EAC所成角的正弦值为![]() .
.
![]() 线段BE上不存在点M,使平面
线段BE上不存在点M,使平面![]() 平面DFM.
平面DFM.
理由如下:
设线段BE上存在点![]() b,
b,![]() ,
,![]() ,
,![]() ,使平面
,使平面![]() 平面DFM,
平面DFM,
则![]() ,
,![]() ,
,![]() ,
,![]() 0,
0,![]() ,
,
设平面DMF的法向量![]() y,
y,![]() ,
,
则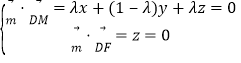 ,取
,取![]() ,得
,得![]() ,
,
![]() 平面
平面![]() 平面DFM,平面EAC的法向量
平面DFM,平面EAC的法向量![]() ,
,
![]() ,解得
,解得![]() ,
,
![]() 线段BE上不存在点M,使平面
线段BE上不存在点M,使平面![]() 平面DFM.
平面DFM.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:高中数学 来源: 题型:
【题目】某公司要在一条笔直的道路边安装路灯,要求灯柱AB与底面垂直,灯杆BC与灯柱AB所在的平面与道路走向垂直,路灯C采用锥形灯罩,射出的管线与平面ABC部分截面如图中阴影所示,![]() 路宽AD=24米,设
路宽AD=24米,设![]()

(1)求灯柱AB的高h(用![]() 表示);
表示);
(2)此公司应该如何设置![]() 的值才能使制作路灯灯柱AB和灯杆BC所用材料的总长度最小?最小值为多少?
的值才能使制作路灯灯柱AB和灯杆BC所用材料的总长度最小?最小值为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在下列四个命题中,错误的有( )
A.坐标平面内的任何一条直线均有倾斜角和斜率
B.直线的倾斜角的取值范围是![]()
C.若一条直线的斜率为![]() ,则此直线的倾斜角为
,则此直线的倾斜角为![]()
D.若一条直线的倾斜角为![]() ,则此直线的斜率为
,则此直线的斜率为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.我国
是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.我国![]() 标准采用世界卫生组织设定的最宽限值,即
标准采用世界卫生组织设定的最宽限值,即![]() 日均值在
日均值在![]() 以下空气质量为优;在
以下空气质量为优;在![]() 之间空气质量为良;在
之间空气质量为良;在![]() 之间空气质量为轻度污染.某市环保局从该市2018年上半年每天的
之间空气质量为轻度污染.某市环保局从该市2018年上半年每天的![]() 日均值数据中随机抽取20天的数据作为样本,将
日均值数据中随机抽取20天的数据作为样本,将![]() 日均值统计如下:
日均值统计如下:
日均值( |
|
|
|
|
|
天数 | 4 | 6 | 5 | 3 | 2 |
(1)在空气质量为轻度污染的数据中,随机抽取两天![]() 日均值数据,求其中恰有一天
日均值数据,求其中恰有一天![]() 日均值数据在
日均值数据在![]() 之间的概率;
之间的概率;
(2)将以上样本数据绘制成频率分布直方图(直接作图):
(3)该市规定:全年![]() 日均值的平均数不高于
日均值的平均数不高于![]() ,则认定该市当年的空气质量达标.现以这20天的
,则认定该市当年的空气质量达标.现以这20天的![]() 日均值的平均数来估计2018年的空气质量情况,试预测该市2018年的空气质量是否达标.
日均值的平均数来估计2018年的空气质量情况,试预测该市2018年的空气质量是否达标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地上年度电价为![]() 元,年用电量为
元,年用电量为![]() 亿千瓦时.本年度计划将电价调至
亿千瓦时.本年度计划将电价调至![]() 之间,经测算,若电价调至
之间,经测算,若电价调至![]() 元,则本年度新增用电量
元,则本年度新增用电量![]() (亿千瓦时)与
(亿千瓦时)与![]() 元成反比例.又当
元成反比例.又当![]() 时,
时,![]() .
.
(1)求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)若每千瓦时电的成本价为![]() 元,则电价调至多少时,本年度电力部门的收益将比上年增加
元,则电价调至多少时,本年度电力部门的收益将比上年增加![]() ?[收益=用电量×(实际电价-成本价)]
?[收益=用电量×(实际电价-成本价)]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学团委组织了“纪念抗日战争胜利73周年”的知识竞赛,从参加竞赛的学生中抽出60名学生,将其成绩(均为整数)分成六段![]() ,
,![]() ,…,
,…,![]() 后,画出如图所示的部分频率分布直方图.观察图形给出的信息,回答下列问题:
后,画出如图所示的部分频率分布直方图.观察图形给出的信息,回答下列问题:

(1)求第四组的频率,并补全这个频率分布直方图;
(2)估计这次竞赛的及格率(60分及以上为及格)和平均分(同一组中的数据用该组区间的中点值代表)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某公司举行的年终庆典活动中,主持人利用随机抽奖软件进行抽奖:由电脑随机生成一张如图所示的3![]() 3表格,其中1格设奖300元,4格各设奖200元,其余4格各设奖100元,点击某一格即显示相应金额.某人在一张表中随机不重复地点击3格,记中奖的总金额为X元.
3表格,其中1格设奖300元,4格各设奖200元,其余4格各设奖100元,点击某一格即显示相应金额.某人在一张表中随机不重复地点击3格,记中奖的总金额为X元.
(1)求概率![]() ;
;
(2)求![]() 的概率分布及数学期望
的概率分布及数学期望![]() .
.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,“共享单车”的出现为市民“绿色出行”提供了极大的方便,某共享单车公司“Mobike”计划在甲、乙两座城市共投资160万元,根据行业规定,每个城市至少要投资30万元,由前期市场调研可知:甲城市收益P与投入![]() 单位:万元
单位:万元![]() 满足
满足![]() ,乙城市收益Q与投入
,乙城市收益Q与投入![]() 单位:万元
单位:万元![]() 满足
满足![]() ,设甲城市的投入为
,设甲城市的投入为![]() 单位:万元
单位:万元![]() ,两个城市的总收益为
,两个城市的总收益为![]() 单位:万元
单位:万元![]() .
.
(1)写出两个城市的总收益![]() 万元
万元![]() 关于甲城市的投入
关于甲城市的投入![]() 万元
万元![]() 的函数解析式,并求出当甲城市投资72万元时公司的总收益;
的函数解析式,并求出当甲城市投资72万元时公司的总收益;
(2)试问如何安排甲、乙两个城市的投资,才能使总收益最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我们学校是一所有着悠久传统文化的学校,我们学校全名叫重庆外国语学校(Chongqing Foreign Language School),又名四川外国语大学附属外国语学校,简称“重外”,1981年,被定为四川省首批办好的重点中学;1997年,被列为重庆市教委首批办好的直属重点中学之一;2001年被国家教育部指定为20%高三学生享有保送资格的全国十三所学校之一,今年我校保送取得了非常辉煌的成绩,目前为止,包括清华大学,北京大学在内目前共保送122名同学,其中北京大学,南开大学,北京外国语大学保送的人数成公差为正数的等差数列,三个学校保送人数之和为24人,三个学校保送学生人数之积为312,则北京外国语大学保送的人数为(以上数据均来自于学校官网)( )
A.10B.11C.13D.14
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com