
设f(x)=x3,等差数列{an}中a3=7,a1+a2+a3=12,记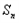 =
=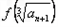 ,令bn=anSn,数列
,令bn=anSn,数列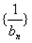 的前n项和为Tn
的前n项和为Tn
(1)求{an}的通项公式和Sn;
(2)求证: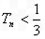 ;
;
(3)是否存在正整数m,n,且1<m<n,使得T1,Tm,Tn成等比数列?若存在,求出m,n的值,若不存在,说明理由.
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:高中数学 来源: 题型:
(08年安徽卷理))在同一平面直角坐标系中,函数![]() 的图象与
的图象与![]() 的图象关于直线
的图象关于直线![]() 对称,而函数
对称,而函数![]() 的图象与
的图象与![]() 的图象关于y轴对称,若
的图象关于y轴对称,若![]() ,则
,则![]() 的值为 【 】
的值为 【 】
(A)-e (B)-![]() (C)e (D)
(C)e (D)![]()
查看答案和解析>>
科目:高中数学 来源:武汉模拟 题型:解答题
| (-1)n |
| an |
查看答案和解析>>
科目:高中数学 来源:浙江模拟 题型:解答题
| 1 |
| 2 |
| 1 |
| b1b2 |
| 1 |
| b2b3 |
| 1 |
| bnbn+1 |
| 25 |
| 51 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 2n+1an | ||
(n+
|
| 2n |
| an |
| 2n |
| cn•cn+1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com