
【题目】已知函数f(x)=(x﹣2)ex+a(x+2)2(x>0).
(1)若f(x)是(0,+∞)的单调递增函数,求实数a的取值范围;
(2)当 ![]() 时,求证:函数f(x)有最小值,并求函数f(x)最小值的取值范围.
时,求证:函数f(x)有最小值,并求函数f(x)最小值的取值范围.
【答案】
(1)解:f'(x)=ex+(x﹣2)ex+2ax+4a,
∵函数f(x)在区间(0,+∞)上单调递增,∴f'(x)≥0在(0,+∞)上恒成立.
∴ex+(x﹣2)ex+2ax+4a≥0,∴ ![]() ,
,
令 ![]() ,
, ![]() ,
,
∴ ![]() ,∴
,∴ ![]()
(2)解:[f'(x)]′=xex+2a>0,
∴y=f'(x)在(0,+∞)上单调递增又f'(0)=4a﹣1<0,f'(1)=6a>0,
∴存在t∈(0,1)使f'(t)=0
∴x∈(0,t)时,f'(x)<0,x∈(t,+∞)时,f'(x)>0,
当x=t时, ![]() 且有f'(t)=et(t﹣1)+2a(t+2)=0,
且有f'(t)=et(t﹣1)+2a(t+2)=0,
∴ ![]() .
.
由(1)知 ![]() 在t∈(0,+∞)上单调递减,
在t∈(0,+∞)上单调递减, ![]() ,且
,且 ![]() ,
,
∴t∈(0,1).
∴ ![]() ,
, ![]() ,
,
∴f(1)<f(t)<f(0),﹣e<f(t)<﹣1,
∴f(x)的最小值的取值范围是(﹣e,﹣1)
【解析】(1)求出函数的导数f'(x)=ex+(x﹣2)ex+2ax+4a,通过f'(x)≥0在(0,+∞)上恒成立.得到 ![]() ,构造函数,利用导函数的单调性以及最值求解即可.(2)通过[f'(x)]′=xex+2a>0,数码y=f'(x)在(0,+∞)上单调递增,利用零点判定定理说明存在t∈(0,1)使f'(t)=0,判断x=t,
,构造函数,利用导函数的单调性以及最值求解即可.(2)通过[f'(x)]′=xex+2a>0,数码y=f'(x)在(0,+∞)上单调递增,利用零点判定定理说明存在t∈(0,1)使f'(t)=0,判断x=t, ![]() ,推出
,推出 ![]() .即
.即 ![]() 在t∈(0,+∞)上单调递减,通过求解函数的最值,求解f(x)的最小值的取值范围.
在t∈(0,+∞)上单调递减,通过求解函数的最值,求解f(x)的最小值的取值范围.
【考点精析】解答此题的关键在于理解利用导数研究函数的单调性的相关知识,掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减.
在这个区间单调递减.


科目:高中数学 来源: 题型:
【题目】已知函数![]() ,若
,若![]()
(1)求![]() 的值,并写出函数
的值,并写出函数![]() 的最小正周期(不需证明);
的最小正周期(不需证明);
(2)是否存在正整数![]() ,使得函数
,使得函数![]() 在区间
在区间![]() 内恰有
内恰有![]() 个零点?若存在,求出
个零点?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)= ![]() ,若f(a)=f(b)=f(c)=f(d),其中a,b,c,d互不相等,则对于命题p:abcd∈(0,1)和命题q:a+b+c+d∈[e+e﹣1﹣2,e2+e﹣2﹣2)真假的判断,正确的是( )
,若f(a)=f(b)=f(c)=f(d),其中a,b,c,d互不相等,则对于命题p:abcd∈(0,1)和命题q:a+b+c+d∈[e+e﹣1﹣2,e2+e﹣2﹣2)真假的判断,正确的是( )
A.p假q真
B.p假q假
C.p真q真
D.p真q假
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD为正方形,PA⊥底面ABCD,AD=AP,E为棱PD中点. 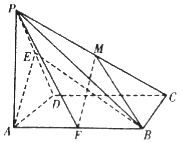
(1)求证:PD⊥平面ABE;
(2)若F为AB中点, ![]() ,试确定λ的值,使二面角P﹣FM﹣B的余弦值为-
,试确定λ的值,使二面角P﹣FM﹣B的余弦值为- ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】徐州市为加快新老城区的融合并进一步缓解交通压力,现经过食品城至新城区(昆仑大道)和食品城至高速入口(迎宾大道),分别修建地铁2号线和快速通道,如图,已知两条公路夹角为60°,为了便于施工拟在两条公路之间的区域内建一混凝土搅拌站P,并分别在两条公路边上建两个中转站M、N (异于点A),要求PM=PN=MN=2(单位:千米).![]()
(1) ![]()
(2)问![]() 为多大时,使得混凝土搅拌站产生的噪声对食品城的影响最小(即搅拌站与食品城的距离最远).
为多大时,使得混凝土搅拌站产生的噪声对食品城的影响最小(即搅拌站与食品城的距离最远).

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(x﹣2)ex+a(x+2)2(x>0).
(1)若f(x)是(0,+∞)的单调递增函数,求实数a的取值范围;
(2)当 ![]() 时,求证:函数f(x)有最小值,并求函数f(x)最小值的取值范围.
时,求证:函数f(x)有最小值,并求函数f(x)最小值的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中
,其中![]() ,记函数
,记函数![]() 的定义域为
的定义域为![]() .
.
(1)求函数![]() 的定义域
的定义域![]() ;
;
(2)若函数![]() 的最大值为2,求
的最大值为2,求![]() 的值;
的值;
(3)若对于![]() 内的任意实数
内的任意实数![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com