
【题目】如图,分别过椭圆![]() 左、右焦点
左、右焦点![]() 的动直线
的动直线![]() 相交于
相交于![]() 点,与椭圆
点,与椭圆![]() 分别交于
分别交于![]() 与
与![]() 不同四点,直线
不同四点,直线![]() 的斜率
的斜率![]() 满足
满足![]() , 已知
, 已知![]() 与
与![]() 轴重合时,
轴重合时, ![]() .
.
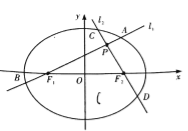
(1)求椭圆![]() 的方程;
的方程;
(2)是否存在定点![]() 使得
使得![]() 为定值,若存在,求出
为定值,若存在,求出![]() 点坐标并求出此定值,若不存在,
点坐标并求出此定值,若不存在,
说明理由.
【答案】(1)![]() ;(2)存在,
;(2)存在,![]() ,
,![]() ,
,![]() .
.
【解析】
试题分析:(1)当![]() 与
与![]() 轴重合时,
轴重合时,![]() 垂直于
垂直于![]() 轴,得
轴,得![]() ,得
,得![]() ,
,![]() 从而得椭圆的方程;(2)由题目分析如果存两定点,则
从而得椭圆的方程;(2)由题目分析如果存两定点,则![]() 点的轨迹是椭圆或者双曲线 ,所以把
点的轨迹是椭圆或者双曲线 ,所以把![]() 坐标化,可得
坐标化,可得![]() 点的轨迹是椭圆,从而求得定点
点的轨迹是椭圆,从而求得定点![]() 和点
和点![]() .
.
试题解析:![]() 当
当![]() 与
与![]() 轴重合时,
轴重合时,![]() , 即
, 即![]() ,所以
,所以![]() 垂直于
垂直于![]() 轴,得
轴,得![]() ,
,![]() ,, 得
,, 得![]() ,
,![]() 椭圆
椭圆![]() 的方程为
的方程为![]() .
.
![]() 焦点
焦点![]() 坐标分别为
坐标分别为![]() , 当直线
, 当直线![]() 或
或![]() 斜率不存在时,
斜率不存在时,![]() 点坐标为
点坐标为![]() 或
或![]() ;
;
当直线![]()
![]() 斜率存在时,设斜率分别为
斜率存在时,设斜率分别为![]() , 设
, 设![]()
![]() 由
由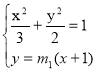 , 得:
, 得:
![]() , 所以:
, 所以: ![]() ,
,![]() , 则:
, 则:
![]()
![]() . 同理:
. 同理:![]()
![]() , 因为
, 因为
![]() , 所以
, 所以![]()
![]() , 即
, 即![]() , 由题意知
, 由题意知![]() , 所以
, 所以
![]() , 设
, 设![]() ,则
,则![]() ,即
,即![]() ,由当直线
,由当直线![]() 或
或![]() 斜率不存在时,
斜率不存在时,![]() 点坐标为
点坐标为![]() 或
或![]() 也满足此方程,所以点
也满足此方程,所以点![]() 在椭圆
在椭圆![]() 上.存在点
上.存在点![]() 和点
和点![]() ,使得
,使得![]() 为定值,定值为
为定值,定值为![]() .
.


 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:高中数学 来源: 题型:
【题目】设全集U=R,集合A={x|1≤x<4},B={x|2a≤x<3-a}.
(1)若a=-2,求B∩A,B∩(UA);(2)若A∪B=A,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某儿童玩具生产厂一车间计划每天生产遥控小车模型、遥控飞机模型、遥控火车模型这三种玩具共![]() 个,生产一个遥控小车模型需
个,生产一个遥控小车模型需![]() 分钟,生产一个遥控飞机模型需
分钟,生产一个遥控飞机模型需![]() 分钟,生产一个遥控火车模型需
分钟,生产一个遥控火车模型需![]() 分钟,已知总生产时间不超过
分钟,已知总生产时间不超过![]() 分钟,若生产一个遥控小车模型可获利
分钟,若生产一个遥控小车模型可获利![]() 元,生产一个遥控飞机模型可获利
元,生产一个遥控飞机模型可获利![]() 元,生产一个遥控火车模型可获利
元,生产一个遥控火车模型可获利![]() 元,该公司合理分配生产任务可使每天的利润最大,则最大利润是__________元
元,该公司合理分配生产任务可使每天的利润最大,则最大利润是__________元
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某险种的基本保费为![]() (单位:元),继续购买该险种的投保人称为续保人,续保人本年度的保费与其
(单位:元),继续购买该险种的投保人称为续保人,续保人本年度的保费与其
上年度出险次数的关联如下:
上年度出险次数 | 0 | 1 | 2 | 3 | 4 |
|
保费 |
|
|
|
|
|
|
随机调查了该险种的200名续保人在一年内的出险情况,得到如下统计表:
出险次数 | 0 | 1 | 2 | 3 | 4 |
|
频数 | 60 | 50 | 30 | 30 | 20 | 10 |
(1)记A为事件:“一续保人本年度的保费不高于基本保费”.求![]() 的估计值;
的估计值;
(2)记B为事件:“一续保人本年度的保费高于基本保费但不高于基本保费的160%”.求![]() 的估计值;
的估计值;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙、丙三台机床各自独立地加工同一种零件,已知甲机床加工的零件是一等品而乙机床加工的零件不是一等品的概率是![]() ,乙机床加工的零件是一等品而丙机床加工的零件不是一等品的概率是
,乙机床加工的零件是一等品而丙机床加工的零件不是一等品的概率是![]() ,甲、乙两台机床加工的零件都是一等品的概率是
,甲、乙两台机床加工的零件都是一等品的概率是![]() .
.
(1)分别求甲、乙、丙三台机床各自加工的零件是一等品的概率;
(2)从甲、乙、丙三台机床加工的零件中各取一个检验,求至少有一个一等品的概率;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A.因为![]() ,所以
,所以![]() 是函数
是函数![]() 的一个周期;
的一个周期;
B.因为![]() ,所以
,所以![]() 是函数
是函数![]() 的最小正周期;
的最小正周期;
C.因为![]() 时,等式
时,等式![]() 成立,所以
成立,所以![]() 是函数
是函数![]() 的一个周期;
的一个周期;
D.因为![]() ,所以
,所以![]() 不是函数
不是函数![]() 的一个周期.
的一个周期.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在上海高考改革方案中,要求每位高中生必须在物理、化学、生物、政治、历史、地理6门学科(3门理科,3门文科)中选择3门学科参加等级考试,小李同学受理想中的大学专业所限,决定至少选择一门理科学科,那么小李同学的选科方案有________种.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com