练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】调查了某地若干户家庭的年收入x(单位：万元)和年饮食支出y(单位：万元)，调查显示年收入x与年饮食支出y具有线性相关关系，并由调查数据得到y对x的回归直线方程： ＝0. 254x＋0. 321. 由回归直线方程可知，家庭年收入每增加1万元，年饮食支出平均增加万元.

    【答案】0.254
    【解析】当 变为 时， =0.245(x+1)+0.321=0.245x+0.321+0.245，而0.245x+0.321+0.245-（0.245x+0.321）=0.245.因此家庭年收入每增加1万元，年饮食支出平均增加0.245万元，本题填写0.245.由题意可知，当x变为x+1时，将x+1代入回归直线方程，由此可以得到年饮食的平均增加。

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）= ，则y=f（x）的图象大致为（ ）
    A.
    B.
    C.
    D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数 ．
    （1）若曲线y=f（x）在P（1，f（1））处的切线平行于直线y=﹣x+1，求函数y=f（x）的单调区间；
    （2）若a＞0，且对任意x∈（0，2e]时，f（x）＞0恒成立，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知f（x）=|ax﹣4|﹣|ax+8|，a∈R
    （Ⅰ）当a=2时，解不等式f（x）＜2；
    （Ⅱ）若f（x）≤k恒成立，求k的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在三棱锥 中，平面 平面 ， 为等边三角形， 且 ， 分别为 的中点.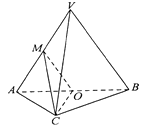

    （1）求证： 平面 .
    （2）求证：平面 平面 .
    （3）求三棱锥 的体积.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）= x3﹣ax2+（a2﹣1）x+b（a，b∈R），其图象在点（1，f（1））处的切线方程为x+y﹣3=0．
    （1）求a，b的值；
    （2）求函数f（x）的单调区间，并求出f（x）在区间[﹣2，4]上的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在直角梯形ABCD中，AB⊥AD，AD∥BC，AB=BC=2AD=2，E，F分别为BC，CD的中点，以A为圆心，AD为半径的圆交AB于G，点P在 上运动（如图）．若 =λ +μ ，其中λ，μ∈R，则6λ+μ的取值范围是（ ）
    A.[1， ]
    B.[ ，2 ]
    C.[2，2 ]
    D.[1，2 ]

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱锥 中，平面PAD⊥ABCD，AB=AD，∠BAD=60°，E，F分别是AP，AD的中点.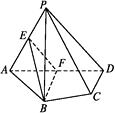

    求证：
    （1）直线EF∥平面PCD；
    （2）平面BEF⊥平面PAD.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】判定下列函数的奇偶性．
    （1）f（x）＝ ；
    （2）f（x）＝ ；
    （3）f（x）＝ ；
    （4）f（x）＝|x＋1|＋|x－1|.

    查看答案和解析>>

    同步练习册答案