
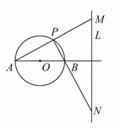
如图,已知圆O的直径AB=4,定直线L到圆心的距离为4,且直线L垂直于直线AB.点P是圆O上异于A、B的任意一点,直线PA、PB分别交L于M、N点.
(1)若∠PAB=30°,求以MN为直径的圆的方程;
(2)当点P变化时,求证:以MN为直径的圆必过AB上一定点.
建立如图所示的直角坐标系,⊙O的方程为x2+y2=4,
直线L的方程为x=4.
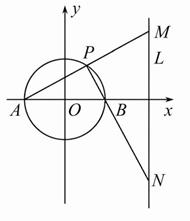 (1)当点P在x轴上方时,
(1)当点P在x轴上方时,
∵∠PAB=30°,
∴点P的坐标为(1,![]() ),
),
∴lAP:y=![]() (x+2),
(x+2),
lBP:y=-![]() (x-2).
(x-2).
将x=4代入,得M(4,2![]() ),N(4,-2
),N(4,-2![]() ).
).
∴MN的中点坐标为(4,0),MN=4![]() .
.
∴以MN为直径的圆的方程为(x-4)2+y2=12.
同理,当点P在x轴下方时,所求圆的方程仍是(x-4)2+y2=12.
(2)设点P的坐标为(x0,y0),∴x![]() +y
+y![]() =4(y0≠0),
=4(y0≠0),
∴y![]() =4-x
=4-x![]() .
.
∵lPA:y=![]() (x+2),lPB:y=
(x+2),lPB:y=![]() (x-2),
(x-2),
将x=4代入,得yM=![]() ,
,![]()
yN=![]() ,∴M(4,
,∴M(4,![]() ),N(4,
),N(4,![]() ),
),
MN=|![]() -
-![]() |=
|=![]() .
.
MN的中点坐标为(4,-![]() ).
).
以MN为直径![]() 的圆O′截x轴的线段长度为
的圆O′截x轴的线段长度为
2![]() =
=![]()
![]()
=![]()
![]() =
=![]() |y0|=4
|y0|=4![]() ,为定值.
,为定值.
∴⊙O′必过AB上一定点(4-2![]() ,0).
,0).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
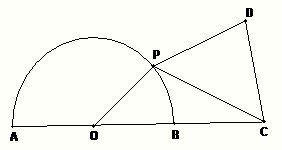 如图:已知圆O的直径是2,点C在直径AB的延长线上,BC=1,点P是圆O上的一个动点,以PC为边作正三角形PCD,且点D与圆心分别在PC的两侧,求四边形OPDC面积的最大值.
如图:已知圆O的直径是2,点C在直径AB的延长线上,BC=1,点P是圆O上的一个动点,以PC为边作正三角形PCD,且点D与圆心分别在PC的两侧,求四边形OPDC面积的最大值.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,已知圆O的直径AB=4,定直线L到圆心的距离为4,且直线L垂直直线AB.点P是圆O上异于A、B的任意一点,直线PA、PB分别交L与M、N点.
如图,已知圆O的直径AB=4,定直线L到圆心的距离为4,且直线L垂直直线AB.点P是圆O上异于A、B的任意一点,直线PA、PB分别交L与M、N点.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,已知圆O的直径AB长度为4,点D为线段AB上一点,且AD=
如图,已知圆O的直径AB长度为4,点D为线段AB上一点,且AD=| 1 |
| 3 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
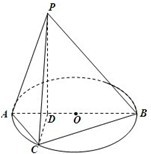 (2013•佛山一模)如图,已知圆O的直径AB长度为4,点D为线段AB上一点,且AD=
(2013•佛山一模)如图,已知圆O的直径AB长度为4,点D为线段AB上一点,且AD=| 1 |
| 3 |
| 3 |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年河北衡水中学高三第一次模拟考试文科数学试卷(解析版) 题型:解答题
(本题12分)
如图,已知圆O的直径AB=4,定直线L到圆心的距离为4,且直线L垂直直线AB。点P是圆O上异于A、B的任意一点,直线PA、PB分别交L与M、N点。

(Ⅰ)若∠PAB=30°,求以MN为直径的圆方程;
(Ⅱ)当点P变化时,求证:以MN为直径的圆必过圆O内的一定点。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com