
ΓΨΧβΡΩΓΩΤτΕΪ –’ΰΗ°Ρβ‘ΎΒϊΚΰΫ®“ΜΗω¬Ο”ΈΙέΙβœνΡΩ,…ηΦΤΖΫΑΗ»γœ¬ΘΚ»γΆΦΥυ ΨΒΡ‘≤O «‘≤–ΈΚΰΒΡ±ΏΫγ,―ΊœΏΕΈAB,BC,CD,DAΫ®“ΜΗωΙέΨΑ≥Λά»,Τδ÷–A,B,C,D «ΙέΨΑ≥Λά»ΒΡΥΡΗω≥ω»κΩΎ«“ΕΦ‘Ύ‘≤O…œΘ§“―÷ΣΘΚBC=12ΑΌΟΉ,AB=8ΑΌΟΉ,‘ΎΚΰ÷–P¥ΠΚΆΚΰ±ΏD¥ΠΗςΫ®“ΜΗωΙέΨΑΆΛ,«“ΥϋΟ«ΙΊ”Ύ÷±œΏACΕ‘≥Τ,‘ΎΚΰΟφΫ®“ΜΧθΙέΨΑ«≈APC.ΙέΨΑΆΛΒΡ¥σ–ΓΓΔΙέΨΑ≥Λά»ΓΔΙέΨΑ«≈ΒΡΩμΕ»ΨυΚω¬‘≤ΜΦΤΘ§…η![]() Θ°
Θ°
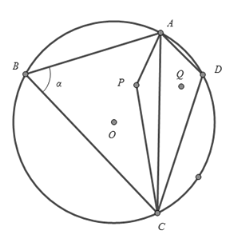
Θ®1Θ©»τΙέΨΑ≥Λά»ADΘΫ4ΑΌΟΉΘ§CD=ABΘ§«σ”…ΙέΨΑ≥Λά»ΥυΈß≥…ΒΡΥΡ±Ώ–ΈABCDΡΎΒΡΚΰΟφΟφΜΐΘΜ
Θ®2Θ©Β±![]() ±Θ§«σ»ΐΫ«–Έ«χ”ρADCΡΎΒΡΚΰΟφΟφΜΐΒΡΉν¥σ÷ΒΘΜ
±Θ§«σ»ΐΫ«–Έ«χ”ρADCΡΎΒΡΚΰΟφΟφΜΐΒΡΉν¥σ÷ΒΘΜ
Θ®3Θ©»τCD=8ΑΌΟΉ«“ΙφΜ°Ϋ®ΆΛΒψP‘Ύ»ΐΫ«–ΈABC«χ”ρΡΎΘ®≤ΜΑϋά®±ΏΫγΘ©Θ§ ‘≈–ΕœΥΡ±Ώ–ΈABCPΡΎΚΰΟφΟφΜΐ «Ζώ”–Ήν¥σ÷ΒΘΩ»τ”–Θ§«σ≥ωΉν¥σ÷ΒΘ§≤Δ–¥≥ω¥Υ ±![]() ΒΡ÷ΒΘΜ»τΟΜ”–Θ§«κΥΒΟςάμ”…Θ°
ΒΡ÷ΒΘΜ»τΟΜ”–Θ§«κΥΒΟςάμ”…Θ°
ΓΨ¥πΑΗΓΩΘ®1Θ©![]() ΤΫΖΫΑΌΟΉΘΜΘ®2Θ©
ΤΫΖΫΑΌΟΉΘΜΘ®2Θ©![]() ΤΫΖΫΑΌΟΉΘΜΘ®3Θ©Β±
ΤΫΖΫΑΌΟΉΘΜΘ®3Θ©Β±![]() =
=![]() ±Θ§ΥΡ±Ώ–ΈABCPΡΎΒΡΚΰΟφΟφΜΐ»ΓΒΫΉν¥σ÷ΒΘ§ Ήν¥σ÷ΒΈΣ32ΤΫΖΫΑΌΟΉ.
±Θ§ΥΡ±Ώ–ΈABCPΡΎΒΡΚΰΟφΟφΜΐ»ΓΒΫΉν¥σ÷ΒΘ§ Ήν¥σ÷ΒΈΣ32ΤΫΖΫΑΌΟΉ.
ΓΨΫβΈωΓΩ
Θ®1Θ©Ζ÷±π‘Ύ![]() ΚΆ
ΚΆ![]() ÷–‘Υ”Ο”ύœ“Ε®άμΘ§«σ≥ω
÷–‘Υ”Ο”ύœ“Ε®άμΘ§«σ≥ω![]() Θ§ΫχΕχΩ…ΒΟ
Θ§ΫχΕχΩ…ΒΟ![]() ΚΆ
ΚΆ![]() Θ§ΗυΨί
Θ§ΗυΨί![]() Φ¥Ω…ΒΟΫαΙϊΘΜΘ®2Θ©‘Ύ
Φ¥Ω…ΒΟΫαΙϊΘΜΘ®2Θ©‘Ύ![]() ÷–Θ§Ω…ΒΟ
÷–Θ§Ω…ΒΟ![]() Θ§Νν
Θ§Νν![]() Θ§
Θ§![]() Θ§‘Ύ
Θ§‘Ύ![]() ÷–Θ§‘Υ”Ο”ύœ“Ε®άμΩ…ΒΟ
÷–Θ§‘Υ”Ο”ύœ“Ε®άμΩ…ΒΟ![]() Θ§”…Μυ±Ψ≤ΜΒ» ΫΩ…ΒΟ
Θ§”…Μυ±Ψ≤ΜΒ» ΫΩ…ΒΟ![]() Θ§”…
Θ§”…![]() Φ¥Ω…ΒΟΫαΙϊΘΜΘ®3Θ©œ»«σ≥ω
Φ¥Ω…ΒΟΫαΙϊΘΜΘ®3Θ©œ»«σ≥ω![]() Θ§ΦΤΥψ≥ω
Θ§ΦΤΥψ≥ω![]() Θ§ΫχΕχΩ…ΒΟΫαΙϊ.
Θ§ΫχΕχΩ…ΒΟΫαΙϊ.
ΫβΘΚΘ®1Θ©ΓΏΥΡ±Ώ–ΈABCDΡΎΫ””Ύ‘≤OΘ§Γύ![]() ABC+
ABC+![]() ADC=
ADC=![]()
‘Ύ![]() ÷–Θ§
÷–Θ§![]()
‘Ύ![]() ÷–Θ§
÷–Θ§![]()
ΫβΒΟ![]() Θ§Γύ
Θ§Γύ![]()
Γύ![]()
Θ®ΤΫΖΫΑΌΟΉΘ©
¥πΘΚΥΡ±Ώ–ΈABCDΡΎΒΡΚΰΟφΟφΜΐ «![]() ΤΫΖΫΑΌΟΉ.
ΤΫΖΫΑΌΟΉ.
Θ®2Θ©ΓΏ![]() =60
=60![]() Θ§Γύ‘Ύ
Θ§Γύ‘Ύ![]() ÷–Θ§
÷–Θ§![]() =112
=112
Νν![]() Θ§
Θ§![]() Θ§ ‘Ύ
Θ§ ‘Ύ![]() ÷–Θ§
÷–Θ§![]() =112
=112
Γύ![]() =112
=112
ΓΏ![]()
Γύ![]() Θ®Β±«“ΫωΒ±x=y ±Θ§»ΓΒ»Κ≈Θ©
Θ®Β±«“ΫωΒ±x=y ±Θ§»ΓΒ»Κ≈Θ©
ΓΏ![]()
Γύ![]() Θ®ΤΫΖΫΑΌΟΉΘ©
Θ®ΤΫΖΫΑΌΟΉΘ©
¥πΘΚ»ΐΫ«–Έ«χ”ρADCΡΎΒΡΚΰΟφΟφΜΐΉν¥σ÷Β![]() ΤΫΖΫΑΌΟΉΘ°
ΤΫΖΫΑΌΟΉΘ°
Θ®3Θ©ΓΏΒψPΚΆΒψDΙΊ”Ύ÷±œΏACΕ‘≥ΤΘ§
Γύ![]() APC=
APC=![]() ADCȧPC=CD=8
ADCȧPC=CD=8
”…Θ®1Θ©÷Σ![]() ABC+
ABC+![]() ADC=
ADC=![]() Θ§Γύ
Θ§Γύ![]() ABC+
ABC+![]() APC=
APC=![]()
ΓΏ![]() ABC=
ABC=![]() Θ§Γύ
Θ§Γύ![]() APC=
APC=![]()
![]()
ΓΏΒψP‘Ύ![]() «χ”ρΡΎ
«χ”ρΡΎ
Γύ![]() Θ§Γύ
Θ§Γύ![]()
ΓΏ‘Ύ![]() ÷–Θ§
÷–Θ§![]()
‘Ύ![]() ÷–Θ§
÷–Θ§![]()
Γύ![]()
ΫβΒΟ![]() Μρ
Μρ![]() Θ®…α»ΞΘ©
Θ®…α»ΞΘ©
![]()
![]()
ΓΏ![]() Θ§ΓύΥΡ±Ώ–ΈABCPΡΎΒΡΚΰΟφΟφΜΐ”–Ήν¥σ÷ΒΘ§
Θ§ΓύΥΡ±Ώ–ΈABCPΡΎΒΡΚΰΟφΟφΜΐ”–Ήν¥σ÷ΒΘ§
¥πΘΚΒ±![]() =
=![]() ±Θ§ΥΡ±Ώ–ΈABCPΡΎΒΡΚΰΟφΟφΜΐ»ΓΒΫΉν¥σ÷ΒΘ§Ήν¥σ÷ΒΈΣ32ΤΫΖΫΑΌΟΉ
±Θ§ΥΡ±Ώ–ΈABCPΡΎΒΡΚΰΟφΟφΜΐ»ΓΒΫΉν¥σ÷ΒΘ§Ήν¥σ÷ΒΈΣ32ΤΫΖΫΑΌΟΉ


 ‘ΡΕΝΩλ≥ΒœΒΝ–¥πΑΗ
‘ΡΕΝΩλ≥ΒœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷Σ ΐΝ–1Θ§1Θ§2Θ§1Θ§2Θ§4Θ§1Θ§2Θ§4Θ§8Θ§1Θ§2Θ§4Θ§8Θ§16Θ§Γ≠Θ§Τδ÷–ΒΎ“Μœν «![]() Θ§Ϋ”œ¬ά¥ΒΡΝΫœν «
Θ§Ϋ”œ¬ά¥ΒΡΝΫœν «![]() Θ§
Θ§![]() Θ§‘ΌΫ”œ¬ά¥ΒΡ»ΐœν «
Θ§‘ΌΫ”œ¬ά¥ΒΡ»ΐœν «![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§“ά¥ΥάύΆΤΘ§»τΗΟ ΐΝ–«Α
Θ§“ά¥ΥάύΆΤΘ§»τΗΟ ΐΝ–«Α![]() œνΚΆ
œνΚΆ![]() ¬ζΉψΘΚΔΌ
¬ζΉψΘΚΔΌ![]() ΔΎ
ΔΎ![]() «2ΒΡ’ϊ ΐ¥ΈΟίΘ§‘ρ¬ζΉψΧθΦΰΒΡΉν–ΓΒΡ
«2ΒΡ’ϊ ΐ¥ΈΟίΘ§‘ρ¬ζΉψΧθΦΰΒΡΉν–ΓΒΡ![]() ΈΣ
ΈΣ
A. 21B. 91C. 95D. 10
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ °Εΰ…ζ–ΛΘ§”÷≥Τ °Εΰ τœύΘ§÷–ΙζΙ≈»ΥΡΟ °Εΰ÷÷Ε·Έοά¥≈δ °ΕΰΒΊ÷ßΘ§Ήι≥…Ή” σΓΔ≥σ≈ΘΓΔ“ζΜΔΓΔΟ°ΆΟΓΔ≥ΫΝζΓΔΥ»…ΏΓΔΈγ¬μΓΔΈ¥―ρΓΔ…ξΚοΓΔ”œΦΠΓΔ–γΙΖΓΔΚΞ÷μ °Εΰ τœύΓΘœ÷”– °Εΰ…ζ–ΛΦΣœιΈοΗς“ΜΦΰΘ§ΦΉΓΔ““ΓΔ±ϊ»ΐΈΜΆ§―ß“Μ¥ΈΥφΜζ≥ι»Γ“ΜΦΰΉςΈΣάώΈοΘ§ΦΉΆ§―ßœ≤ΜΕ¬μΓΔ≈ΘΘ§““Ά§―ßœ≤ΜΕ¬μΓΔΝζΓΔΙΖΘ§±ϊΆ§―ß≥ΐΝΥ σ≤Μœ≤ΜΕΆβΤδΥϊΒΡΕΦœ≤ΜΕΘ§‘ρ’β»ΐΈΜΆ§―ß≥ι»ΓΒΡάώΈοΕΦœ≤ΜΕΒΡΗ≈¬ «( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ![]() ÷–Θ§ΙΐΕ®Βψ
÷–Θ§ΙΐΕ®Βψ![]() Ής÷±œΏ”κ≈ΉΈοœΏ
Ής÷±œΏ”κ≈ΉΈοœΏ![]() œύΫΜ”Ύ
œύΫΜ”Ύ![]() ΓΔ
ΓΔ![]() ΝΫΒψΘ°
ΝΫΒψΘ°
Θ®1Θ©“―÷Σ![]() Θ§»τΒψ
Θ§»τΒψ![]() «Βψ
«Βψ![]() ΙΊ”ΎΉχ±ξ‘≠Βψ
ΙΊ”ΎΉχ±ξ‘≠Βψ![]() ΒΡΕ‘≥ΤΒψΘ§«σ
ΒΡΕ‘≥ΤΒψΘ§«σ![]() ΟφΜΐΒΡΉν–Γ÷ΒΘΜ
ΟφΜΐΒΡΉν–Γ÷ΒΘΜ
Θ®2Θ© «Ζώ¥φ‘Ύ¥Ι÷±”Ύ![]() ÷αΒΡ÷±œΏ
÷αΒΡ÷±œΏ![]() Θ§ ΙΒΟ
Θ§ ΙΒΟ![]() ±Μ“‘
±Μ“‘![]() ΈΣ÷±ΨΕΒΡ‘≤ΫΊΒΟΒΡœ“≥ΛΚψΈΣΕ®÷ΒΘΩ»τ¥φ‘ΎΘ§«σ≥ω
ΈΣ÷±ΨΕΒΡ‘≤ΫΊΒΟΒΡœ“≥ΛΚψΈΣΕ®÷ΒΘΩ»τ¥φ‘ΎΘ§«σ≥ω![]() ΒΡΖΫ≥ΧΘΜ»τ≤Μ¥φ‘ΎΘ§ΥΒΟςάμ”…Θ°
ΒΡΖΫ≥ΧΘΜ»τ≤Μ¥φ‘ΎΘ§ΥΒΟςάμ”…Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΚ· ΐ![]()
Θ®ΔώΘ©»τ![]() Θ§«σ«ζœΏ
Θ§«σ«ζœΏ![]() ‘ΎΒψ
‘ΎΒψ![]() ¥ΠΒΡ«–œΏΖΫ≥ΧΘΜ
¥ΠΒΡ«–œΏΖΫ≥ΧΘΜ
Θ®ΔρΘ©»τ![]() ‘Ύ
‘Ύ![]() …œΚψ≥…ΝΔΘ§«σ Β ΐ
…œΚψ≥…ΝΔΘ§«σ Β ΐ![]() ΒΡ»Γ÷ΒΖΕΈßΘΜ
ΒΡ»Γ÷ΒΖΕΈßΘΜ
Θ®ΔσΘ©»τ ΐΝ–![]() ΒΡ«Α
ΒΡ«Α![]() œνΚΆ
œνΚΆ![]() Θ§
Θ§ ![]() Θ§«σ÷ΛΘΚ ΐΝ–
Θ§«σ÷ΛΘΚ ΐΝ–![]() ΒΡ«Α
ΒΡ«Α![]() œνΚΆ
œνΚΆ![]() .
.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ…η ΐΝ–![]() ΒΡ«Α
ΒΡ«Α![]() œνΚΆΈΣ
œνΚΆΈΣ![]() Θ§“―÷Σ
Θ§“―÷Σ![]() .
.
Θ®1Θ©«σ ΐΝ–![]() ΒΡΆ®œνΙΪ ΫΘΜ
ΒΡΆ®œνΙΪ ΫΘΜ
Θ®2Θ©»τΕ‘»Έ“βΒΡ![]() Θ§≤ΜΒ» Ϋ
Θ§≤ΜΒ» Ϋ![]() Κψ≥…ΝΔΘ§«σ Β ΐ
Κψ≥…ΝΔΘ§«σ Β ΐ![]() ΒΡ»Γ÷ΒΖΕΈß.
ΒΡ»Γ÷ΒΖΕΈß.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΗςœνΨυΈΣ’ΐ’ϊ ΐΒΡ ΐΝ–{an}ΒΡ«ΑnœνΚΆΈΣSnΘ§¬ζΉψΘΚSn©¹1+kanΘΫtan2©¹1Θ§nΓί2Θ§nΓ N*Θ®Τδ÷–kΘ§tΈΣ≥Θ ΐΘ©Θ°
Θ®1Θ©»τkΘΫ![]() Θ§tΘΫ
Θ§tΘΫ![]() Θ§ ΐΝ–{an} «Β»≤ν ΐΝ–Θ§«σa1ΒΡ÷ΒΘΜ
Θ§ ΐΝ–{an} «Β»≤ν ΐΝ–Θ§«σa1ΒΡ÷ΒΘΜ
Θ®2Θ©»τ ΐΝ–{an} «Β»±» ΐΝ–Θ§«σ÷ΛΘΚkΘΦtΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷Σ’ΐœν ΐΝ–![]() ΒΡ«Α
ΒΡ«Α![]() œνΚΆΈΣ
œνΚΆΈΣ![]() Θ§«“
Θ§«“![]() Θ§
Θ§![]() Θ§ ΐΝ–
Θ§ ΐΝ–![]() ¬ζΉψ
¬ζΉψ![]() Θ§«“
Θ§«“![]()
Θ®IΘ©«σ ΐΝ–![]() Θ§
Θ§![]() ΒΡΆ®œνΙΪ ΫΘΜ
ΒΡΆ®œνΙΪ ΫΘΜ
Θ®IIΘ©Νν![]() Θ§«σ ΐΝ–
Θ§«σ ΐΝ–![]() ΒΡ«Α
ΒΡ«Α![]() œνΚΆ
œνΚΆ![]() ΓΘ
ΓΘ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ2019ΡξΘ§Κ”±±Β»8 ΓΙΪ≤ΦΝΥΗΏΩΦΗΡΗοΉέΚœΖΫΑΗΫΪ≤…»ΓΓΑ![]() Γ±ΡΘ ΫΘ§Φ¥”οΈΡΓΔ ΐ―ßΓΔ”Δ”ο±ΊΩΦΘ§»ΜΚσΩΦ…ζœ»‘ΎΈοάμΓΔάζ Ζ÷–―Γ‘ώ1Ο≈Θ§‘Ό‘ΎΥΦœκ’ΰ÷ΈΓΔΒΊάμΓΔΜ·―ßΓΔ…ζΈο÷–―Γ‘ώ2Ο≈.ΈΣΝΥΗϋΚΟΫχ––…ζ―ΡΙφΜ°Θ§’≈ΟςΆ§―ßΕ‘ΗΏ“Μ“ΜΡξά¥ΒΡΤΏ¥ΈΩΦ ‘≥…Φ®Ϋχ––Ά≥ΦΤΖ÷ΈωΘ§Τδ÷–ΈοάμΓΔάζ Ζ≥…Φ®ΒΡΨΞ“ΕΆΦ»γΆΦΥυ Ψ.
Γ±ΡΘ ΫΘ§Φ¥”οΈΡΓΔ ΐ―ßΓΔ”Δ”ο±ΊΩΦΘ§»ΜΚσΩΦ…ζœ»‘ΎΈοάμΓΔάζ Ζ÷–―Γ‘ώ1Ο≈Θ§‘Ό‘ΎΥΦœκ’ΰ÷ΈΓΔΒΊάμΓΔΜ·―ßΓΔ…ζΈο÷–―Γ‘ώ2Ο≈.ΈΣΝΥΗϋΚΟΫχ––…ζ―ΡΙφΜ°Θ§’≈ΟςΆ§―ßΕ‘ΗΏ“Μ“ΜΡξά¥ΒΡΤΏ¥ΈΩΦ ‘≥…Φ®Ϋχ––Ά≥ΦΤΖ÷ΈωΘ§Τδ÷–ΈοάμΓΔάζ Ζ≥…Φ®ΒΡΨΞ“ΕΆΦ»γΆΦΥυ Ψ.
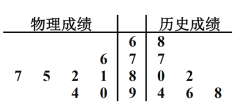
Θ®1Θ©»τ’≈ΟςΆ§―ßΥφΜζ―Γ‘ώ3Ο≈ΙΠΩΈΘ§«σΥϊ―ΓΒΫΈοάμ’ΰ÷ΈΝΫΟ≈ΙΠΩΈΒΡΗ≈¬ ΘΜ
Θ®2Θ© ‘ΗυΨίΨΞ“ΕΆΦΖ÷Έω’≈ΟςΆ§―ß”Π‘ΎΈοάμΚΆάζ Ζ÷–―Γ‘ώΡΡΗω―ßΩΤΘΩ≤Δ≤ϊ ωάμ”….
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com