
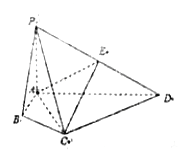
【题目】在四棱锥![]() 中,
中, ![]() 平面
平面![]() ,
, ![]() 是
是![]() 的中点,
的中点, ![]() ,
, ![]() ,
, ![]() .
.
(1)求证: ![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)证明见解析;(2) ![]() .
.
【解析】试题分析:(1)取![]() 的中点
的中点![]() ,连接
,连接![]() ,则
,则![]() ,先根据线面垂直的性质证明
,先根据线面垂直的性质证明![]() ;进而可得
;进而可得![]() ,再由线面判定定理即可证明
,再由线面判定定理即可证明![]() 平面
平面![]() ,从而可得
,从而可得![]() ;(2)建立空间坐标系,分别求出平面
;(2)建立空间坐标系,分别求出平面![]() 与平面
与平面![]() 的的一个法向量,根据空间向量夹角余弦公式,即可求二面角
的的一个法向量,根据空间向量夹角余弦公式,即可求二面角![]() 的余弦值.
的余弦值.
试题解析:(1)取![]() 的中点
的中点![]() ,连接
,连接![]() ,则
,则![]() .
.
因为![]() ,所以
,所以![]() .
.
因为![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,所以
,所以![]() 又
又![]()
所以![]() 平面
平面![]()
因为![]() 平面
平面![]() ,所以
,所以![]() ;又
;又![]() ,所以
,所以![]() ;
;
又因为![]() ,
, ![]() ,所以
,所以![]() 平面
平面![]()
因为![]() 平面
平面![]() ,所以
,所以![]() .
.
(2)以![]() 为原点,建立如图所示的空间直角坐标系
为原点,建立如图所示的空间直角坐标系![]() .
.
则![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]()
![]() ,
, ![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,则
,则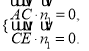 所以
所以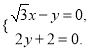
令![]() ,所以
,所以![]() .
.
由(1)知![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,所以
,所以![]() .
.
同理![]() ,所以
,所以![]() 平面
平面![]()
所以平面![]() 的一个法向量
的一个法向量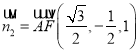 .
.
所以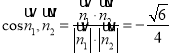 ,
,
由图可知,二面角![]() 为锐角,
为锐角,
所以二面角![]() 的余弦值为
的余弦值为![]() .
.
【方法点晴】本题主要考查线面垂直的判定与性质、利用空间向量求二面角,属于难题.空间向量解答立体几何问题的一般步骤是:(1)观察图形,建立恰当的空间直角坐标系;(2)写出相应点的坐标,求出相应直线的方向向量;(3)设出相应平面的法向量,利用两直线垂直数量积为零列出方程组求出法向量;(4)将空间位置关系转化为向量关系;(5)根据定理结论求出相应的角和距离.


 科学实验活动册系列答案
科学实验活动册系列答案科目:高中数学 来源: 题型:
【题目】某正弦交流电的电压v(单位V)随时间t(单位:s)变化的函数关系是v=120 ![]() sin(100πt﹣
sin(100πt﹣ ![]() ),t∈[0,+∞).
),t∈[0,+∞).
(1)求该正弦交流电电压v的周期、频率、振幅;
(2)若加在霓虹灯管两端电压大于84V时灯管才发光,求在半个周期内霓虹灯管点亮的时间?( 取 ![]() ≈1.4)
≈1.4)
查看答案和解析>>
科目:高中数学 来源: 题型:
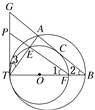
【题目】如图所示,两圆内切于点T,大圆的弦AB切小圆于点C.TA,TB与小圆分别相交于点E,F.FE的延长线交两圆的公切线TP于点P.
求证:(1) ![]() =
=![]() ;
;
(2)AC·PF=BC·PT.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]()
(1)求函数f(x)的最小正周期和图象的对称轴方程.
(2)求函数f(x)的单调增区间.
(3)求函数y=f(x)在区间 ![]() 上的最小值,并求使y=f(x)取得最小值时的x的值.
上的最小值,并求使y=f(x)取得最小值时的x的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() ,
, ![]() 是椭圆
是椭圆![]() 上的两点,椭圆的离心率为
上的两点,椭圆的离心率为![]() ,短轴长为2,已知向量
,短轴长为2,已知向量![]() ,
, ![]() ,且
,且![]() ,
, ![]() 为坐标原点.
为坐标原点.
(1)若直线![]() 过椭圆的焦点
过椭圆的焦点![]() ,(
,( ![]() 为半焦距),求直线
为半焦距),求直线![]() 的斜率
的斜率![]() 的值;
的值;
(2)试问: ![]() 的面积是否为定值?如果是,请给予证明;如果不是,请说明理由.
的面积是否为定值?如果是,请给予证明;如果不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂生产的产品在出厂前都要做质量检测,每一件一等品都能通过检测,每一件二等品通过检测的概率为![]() .现有10件产品,其中6件是一等品,4件是二等品.
.现有10件产品,其中6件是一等品,4件是二等品.
(1)随机选取1件产品,求能够通过检测的概率;
(2)随机选取3件产品,其中一等品的件数记为![]() ,求
,求![]() 的分布列及数学期望..
的分布列及数学期望..
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题p:x∈A,且A={x|a﹣1<x<a+1},命题q:x∈B,且B={x|x2﹣4x+3≥0} (Ⅰ)若A∩B=,A∪B=R,求实数a的值;
(Ⅱ)若p是q的充分条件,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】通过随机询问110名性别不同的中学生是否爱好运动,得到如下的列联表:
男 | 女 | 总计 | |
爱好 | 40 | 20 | 60 |
不爱好 | 20 | 30 | 50 |
总计 | 60 | 50 | 110 |
由K2= ![]() 得,K2=
得,K2= ![]() ≈7.8
≈7.8
P(K2≥k) | 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
参照附表,得到的正确结论是( )
A.在犯错误的概率不超过0.1%的前提下,认为“爱好运动与性别有关”
B.有99%以上的把握认为“爱好运动与性别有关”
C.在犯错误的概率不超过0.1%的前提下,认为“爱好运动与性别无关”
D.有99%以上的把握认为“爱好运动与性别无关”
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com