
【题目】已知函数![]() .
.

(1)如图,设直线![]() 将坐标平面分成
将坐标平面分成![]() 四个区域(不含边界),若函数
四个区域(不含边界),若函数![]() 的图象恰好位于其中一个区域内,判断其所在的区域并求对应的
的图象恰好位于其中一个区域内,判断其所在的区域并求对应的![]() 的取值范围;
的取值范围;
(2)当![]() 时,求证:
时,求证:![]() 且
且![]() ,有
,有![]() .
.
【答案】(1)![]() ,
,![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】试题分析:(1)根据定义域确定只能在3,4区域,再根据![]() 确定只能在4,转化为不等式
确定只能在4,转化为不等式![]() 恒成立,分离变量得
恒成立,分离变量得![]() .利用导数求函数
.利用导数求函数![]() 单调性,根据单调性确定函数最值,即得
单调性,根据单调性确定函数最值,即得![]() 的取值范围;(2)作差函数
的取值范围;(2)作差函数![]() ,再利用二次求导确定
,再利用二次求导确定![]() 为单调递减函数,最后根据
为单调递减函数,最后根据![]() ,得
,得![]() ,即得结论.
,即得结论.
试题解析:(1)函数的定义域为![]() ,且当
,且当![]() 时,
时,![]() .
.
又直线![]() 恰好通过原点,
恰好通过原点,
∴函数![]() 的图象应位于区域Ⅳ内,
的图象应位于区域Ⅳ内,
于是可得![]() ,
,
即![]() .
.
∵![]() ,∴
,∴![]() .
.
令![]() ,则
,则![]() .
.
∴![]() 时,
时,![]() ,
,![]() 单调递增;
单调递增;
![]() 时,
时,![]() ,
,![]() 单调递减.
单调递减.
∴![]()
∴![]() 的取值范围是
的取值范围是![]() .
.
(2)∵![]() ,
,
设![]() ,
,
则![]() ,
,
![]() ,
,
∴![]() ,
,
∴![]() 时
时 ![]() 为单调递减函数,
为单调递减函数,
不妨设![]() ,令
,令![]() (
(![]() ),
),
可得![]() ,
,
![]() ,∵
,∵![]() 且
且![]() 单调递减函数,
单调递减函数,
∴![]() ,∴
,∴![]() ,
,![]() 为单调递减函数,
为单调递减函数,
∴![]() ,
,
即![]() .
.


 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案科目:高中数学 来源: 题型:
【题目】设动点![]() 到定点
到定点![]() 的距离比它到
的距离比它到![]() 轴的距离大
轴的距离大![]() ,记点
,记点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求点![]() 的轨迹方程;
的轨迹方程;
(2)若圆心在曲线![]() 上的动圆
上的动圆![]() 过点
过点![]() ,试证明圆
,试证明圆![]() 与
与![]() 轴必相交,且截
轴必相交,且截![]() 轴所得的弦长为定值.
轴所得的弦长为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正方体![]() 中边长AB为2,P为正方形A1B1C1D1四边上的动点,O为底面正方形ABCD的中心,Q为正方形ABCD内一点,M,N分别为AB,BC上靠近A和C的三等分点,若线段
中边长AB为2,P为正方形A1B1C1D1四边上的动点,O为底面正方形ABCD的中心,Q为正方形ABCD内一点,M,N分别为AB,BC上靠近A和C的三等分点,若线段![]() 与OP相交且互相平分,则点Q的轨迹与线段MN形成的封闭图形的面积为____.
与OP相交且互相平分,则点Q的轨迹与线段MN形成的封闭图形的面积为____.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某篮球比赛采用7局4胜制,即若有一队先胜4局,则此队获胜,比赛就此结束.由于参加比赛的两队实力相当,每局比赛两队获胜的可能性均为![]() .据以往资料统计,第一局比赛组织者可获得门票收入40万元,以后每局比赛门票收入比上一局增加10万元,则组织者在此次比赛中获得的门票收入不少于390万元的概率为________.
.据以往资料统计,第一局比赛组织者可获得门票收入40万元,以后每局比赛门票收入比上一局增加10万元,则组织者在此次比赛中获得的门票收入不少于390万元的概率为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆![]() :
:![]()
![]() 的离心率为
的离心率为![]() ,抛物线
,抛物线![]() :
:![]() 截
截![]() 轴所得的线段长等于
轴所得的线段长等于![]() .
.![]() 与
与![]() 轴的交点为
轴的交点为![]() ,过点
,过点![]() 作直线
作直线![]() 与
与![]() 相交于点
相交于点![]() 直线
直线![]() 分别与
分别与![]() 相交于
相交于![]() .
.
(1)求证:![]() ;
;
(2)设![]() ,
,![]() 的面积分别为
的面积分别为![]() ,若
,若![]()
![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() :
:![]() ,直线
,直线![]() :
:![]() .以极点
.以极点![]() 为原点,极轴为
为原点,极轴为![]() 轴的正半轴建立平面直角坐标系.
轴的正半轴建立平面直角坐标系.
(1)求直线![]() ,
,![]() 的直角坐标方程以及曲线
的直角坐标方程以及曲线![]() 的参数方程;
的参数方程;
(2)已知直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点,直线
两点,直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点,求
两点,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,一个铝合金窗分为上、下两栏,四周框架和中间隔档的材料为铝合金,宽均为6![]() ,上栏与下栏的框内高度(不含铝合金部分)的比为1:2,此铝合金窗占用的墙面面积为28800
,上栏与下栏的框内高度(不含铝合金部分)的比为1:2,此铝合金窗占用的墙面面积为28800![]() ,设该铝合金窗的宽和高分别为
,设该铝合金窗的宽和高分别为![]() ,铝合金窗的透光部分的面积为
,铝合金窗的透光部分的面积为![]() .
.
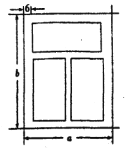
(1)试用![]() 表示
表示![]() ;
;
(2)若要使![]() 最大,则铝合金窗的宽和高分别为多少?
最大,则铝合金窗的宽和高分别为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2018·邯郸一模)若甲、乙两类水果的质量(单位:kg)分别服从正态分布N(μ1,σ2)及N(μ2,σ2),其正态分布的密度曲线如图所示,则下列说法错误的是( )

A. 乙类水果的质量服从的正态分布的参数σ2=64
B. 甲类水果的质量比乙类水果的质量更集中
C. 甲类水果的平均质量μ1=0.4 kg
D. 甲类水果的平均质量比乙类水果的平均质量小
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com