
【题目】三棱锥P﹣ABC中,△ABC是底面,PA⊥PB,PA⊥PC,PB⊥PC,且这四个顶点都在半径为2的球面上,PA=2PB,则这个三棱锥的三个侧棱长的和的最大值为( )
A.16
B.![]()
C.![]()
D.32
【答案】B
【解析】解:∵PA,PB,PC两两垂直,
又∵三棱锥P﹣ABC的四个顶点均在半径为2的球面上,
∴以PA,PB,PC为棱的长方体的对角线即为球的一条直径.
∴16=PA2+PB2+PC2 , 又PA=2PB,∴5PB2+PC2=16,
设PB=![]() ,PC=4sinα,
,PC=4sinα,
则这个三棱锥的三个侧棱长的和PA+PB+PC=3PB+PC=![]() cosα+4sinα=
cosα+4sinα=![]() sin(α+)≤
sin(α+)≤![]() .
.
则这个三棱锥的三个侧棱长的和的最大值为![]() ,
,
故选B.
【考点精析】本题主要考查了棱台的结构特征和球内接多面体的相关知识点,需要掌握①上下底面是相似的平行多边形②侧面是梯形③侧棱交于原棱锥的顶点;球的内接正方体的对角线等于球直径;长方体的外接球的直径是长方体的体对角线长才能正确解答此题.


 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:高中数学 来源: 题型:
【题目】下列四组中的函数f(x)与g(x),是同一函数的是( )
A.f(x)=ln(1﹣x)+ln(1+x),g(x)=ln(1﹣x2)
B.f(x)=lgx2 , g(x)=2lgx
C.f(x)= ![]() ?
? ![]() ,g(x)=
,g(x)= ![]()
D.f(x)= ![]() ,g(x)=x+1
,g(x)=x+1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C所对的边分别为a,b,c,且满足csinA=acosC
(1)求角C大小;
(2)求 ![]() sinA﹣cos(B+
sinA﹣cos(B+ ![]() )的最大值,并求取得最大值时角A,B的大小.
)的最大值,并求取得最大值时角A,B的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小明跟父母、爷爷奶奶一同参加《中国诗词大会》的现场录制,5人坐成一排.若小明的父母至少有一人与他相邻,则不同坐法的总数为
A. 60 B. 72 C. 84 D. 96
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方体ABCD﹣A1B1C1D1中,E为AB中点,F为正方形BCC1B1的中心.
(1)求直线EF与平面ABCD所成角的正切值;
(2)求异面直线A1C与EF所成角的余弦值.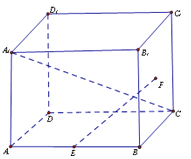
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=﹣x3+ax2﹣x﹣1在(﹣∞,+∞)上是单调函数,则实数a的取值范围是( )
A.[﹣![]() ,
, ![]() ]
]
B.(﹣![]() ,
, ![]() )
)
C.(﹣∞,﹣![]() )∪(
)∪(![]() , +∞)
, +∞)
D.(﹣∞,﹣![]() )∩(
)∩(![]() , +∞)
, +∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题甲:关于x的不等式x2+(a﹣1)x+a2≤0的解集为空集;命题乙:方程x2+ ![]() ax﹣(a﹣4)=0有两个不相等的实根.
ax﹣(a﹣4)=0有两个不相等的实根.
(1)若甲,乙都是真命题,求实数a的取值范围;
(2)若甲,乙中有且只有一个是假命题,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com