
【题目】已知函数![]() 有两个零点
有两个零点![]() ,则下列说法错误的是( )
,则下列说法错误的是( )
A.![]() B.
B.![]() C.有极大值点
C.有极大值点![]() ,且
,且![]() D.
D.![]()
【答案】B
【解析】
对![]() 求导,可得
求导,可得![]() 的极大值点,可得a的取值范围,可判断A选项,同时构造函数
的极大值点,可得a的取值范围,可判断A选项,同时构造函数![]() ,其中
,其中![]() ,可得
,可得![]() ,可得
,可得![]() 的单调性,可判断B、C选项,利用C的结论,可得
的单调性,可判断B、C选项,利用C的结论,可得![]() ,
,![]() ,
, ![]() ,可判断D选项,可得答案.
,可判断D选项,可得答案.
解:由![]() ,可得
,可得![]() ,
,
当![]() 时,
时,![]() ,
,![]()
![]() 在
在![]() 上单调递增,与题意不符;
上单调递增,与题意不符;
当![]() 时,可得当
时,可得当![]() 解得:
解得:![]() ,
,
可得当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
可得当![]() 时,
时,![]() 取得极大值点,且由函数
取得极大值点,且由函数![]() 有两个零点
有两个零点![]() ,
,
可得![]() ,可得
,可得![]() ,综合可得:
,综合可得:![]() ,故A正确;
,故A正确;
由A可得得![]() 的极大值为
的极大值为![]() ,设
,设![]() ,
,
设![]() ,其中
,其中![]() ,可得
,可得![]() ,
,
可得![]() ,
,
可得![]() ,
,
易得当![]() 时候,
时候,![]() ,当
,当![]() ,
,![]() ,
,
故![]() ,
,![]() ,
,
故![]() ,
,![]() ,
,
由![]() ,易得
,易得![]() ,且
,且![]() ,
,
且![]() 时,
时,![]() ,
,![]() 单调递减,故由
单调递减,故由![]() ,
,
可得![]() ,即
,即![]() ,即:有极大值点
,即:有极大值点![]() ,且
,且![]() ,
,
故C正确,B不正确;
由函数![]() 有两个零点
有两个零点![]() ,可得
,可得![]() ,
,![]() ,
,
可得![]() ,
,![]() ,可得
,可得![]() ,
,
由前面可得,![]() ,可得
,可得![]() ,
,
故D正确,
故选:C.


 步步高达标卷系列答案
步步高达标卷系列答案科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的顶点在坐标原点,其焦点
的顶点在坐标原点,其焦点![]() 在
在![]() 轴正半轴上,
轴正半轴上,![]() 为直线
为直线![]() 上一点,圆
上一点,圆![]() 与
与![]() 轴相切(
轴相切(![]() 为圆心),且
为圆心),且![]() ,
,![]() 关于点
关于点![]() 对称.
对称.
(1)求圆![]() 和抛物线
和抛物线![]() 的标准方程;
的标准方程;
(2)过![]() 的直线
的直线![]() 交圆
交圆![]() 于
于![]() ,
,![]() 两点,交抛物线
两点,交抛物线![]() 于
于![]() ,
,![]() 两点,求证:
两点,求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,锐角![]() 的三边互不相等,其垂心为
的三边互不相等,其垂心为![]() ,
,![]() 是边
是边![]() 的中点,直线
的中点,直线![]() ,
,![]() 的外接圆交
的外接圆交![]() 的外接圆于
的外接圆于![]() ,直线
,直线![]() 与
与![]() 的外接圆、
的外接圆、![]() 的外接圆分别交于
的外接圆分别交于![]() 证明:
证明:

(1)![]() 平分
平分![]() ;
;
(2)![]() 三线共点。
三线共点。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义:如果函数![]() 的导函数为
的导函数为![]() ,在区间
,在区间![]() 上存在
上存在![]() ,
,![]() 使得
使得![]() ,
,![]() ,则称
,则称![]() 为区间
为区间![]() 上的“双中值函数“
上的“双中值函数“![]() 已知函数
已知函数![]() 是
是![]() 上的“双中值函数“,则实数m的取值范围是
上的“双中值函数“,则实数m的取值范围是![]()
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正四面体ABCD的棱长为2,球O与四面体的面ABC和面DBC都相切,其切点分别在△ABC和△DBC内(含边界),且球O与棱AD相切.
(1)证明:球O的球心在棱AD的中垂面上;
(2)求球O的半径的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是某公司一种产品的日销售量![]() (单位:百件)关于日最高气温
(单位:百件)关于日最高气温![]() (单位:
(单位:![]() )的散点图.
)的散点图.

数据:
| 13 | 15 | 19 | 20 | 21 |
| 26 | 28 | 30 | 18 | 36 |
(1)请剔除一组数据,使得剩余数据的线性相关性最强,并用剩余数据求日销售量![]() 关于日最高气温
关于日最高气温![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)根据现行《重庆市防暑降温措施管理办法》.若气温超过36度,职工可享受高温补贴.已知某日该产品的销售量为53.1,请用(1)中求出的线性回归方程判断该公司员工当天是否可享受高温补贴?
附: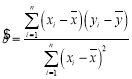 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《易经》是中国传统文化中的精髓,如图是易经八卦(含乾、坤、巽、震、坎、离、艮、兑八卦),每一卦由三根线组成("![]() "表示一根阳线,"
"表示一根阳线,"![]() "表示一根阴线),从八卦中任取两卦,这两卦的六根线中恰有两根阳线,四根阴线的概率为_______.
"表示一根阴线),从八卦中任取两卦,这两卦的六根线中恰有两根阳线,四根阴线的概率为_______.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() 的左焦点为
的左焦点为![]() ,离心率为
,离心率为![]() ,
,![]() 为圆
为圆![]() 的圆心.
的圆心.
(1)求椭圆的方程;
(2)已知过椭圆右焦点![]() 的直线
的直线![]() 交椭圆于
交椭圆于![]() 两点,过
两点,过![]() 且与
且与![]() 垂直的直线
垂直的直线![]() 与圆
与圆![]() 交于
交于![]() 两点,求四边形
两点,求四边形![]() 面积的取值范围.
面积的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com