
如图α⊥β,α∩β=l,A∈α,B∈β,点A在直线l上的射影为A1,点B在l上的射影为B1,已知AB=2,AA1=1,BB1=![]() ,求:
,求:

(1)直线AB分别与平面α,β所成角的大小;
(2)二面角A1-AB-B1的大小.
|
解法一:(1)如图,连接A1B、AB1.
∵α⊥β,α∩β=l,AA1⊥l,BB1⊥l,∴AA1⊥β,BB1⊥α,则∠BAB1、∠ABA1分别是AB与α和β所成的角. Rt△BB1A中,BB1= ∴sin∠BAB1= Rt△AA1B中AA1=1,AB=2. ∴sin∠ABA1= 故AB与平面α,β所成的角分别是45°,30°. (2)∵BB1⊥α, ∴平面ABB1⊥α,在平面α内过A1,作A1E⊥AB1,交AB1于E,则A1E⊥平面AB1B.过E作EF⊥AB交AB于F,连接A1F,则由三垂线定理得A1F⊥AB. ∴∠A1FE就是所求二面角的平面角. 在Rt△ABB1中,∠BAB1=45°, ∴AB1=B1B= ∴Rt△AA1B1中,AA1=A1B1=1. ∴A1E= 在Rt△AA1B中,A1B= 由AA1·A1B=A1F·AB得 A1F= ∴在Rt△A1EF中,sin∠A1FE= ∴二面角A1-AB-B1的大小为arcsin 解法二:(1)同解法一. (2)如下图,建立坐标系,则A1(0,0,0),A(0,0,1),B1(0,1,0),B(
即(x,y,z-1)=t( 要使 即( 2t+t-(1-t)=0,解得t= ∴ 设E为AB1的中点,则点E的坐标为(0, ∴ 又 ∴ ∴∠A1FE为所求二面角的平面角. 又cos∠A1FE= ∴二面角A1-AB-B1的大小为arccos |


 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案科目:高中数学 来源:2014届广东佛山佛山一中高二下第一次段考文科数学试卷(解析版) 题型:填空题
如图,函数y=f(x)的图象在点P处的切线方程是y=-x+8,则f(5)+f′(5)=________.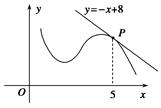
查看答案和解析>>
科目:高中数学 来源:2014届四川省高二上学期期中考试数学试卷(解析版) 题型:填空题
(理)如图,将∠B=,边长为1的菱形ABCD沿对角线AC折成大小等于θ的二面角B-AC-D,若θ∈[,],M、N分别为AC、BD的中点,则下面的四种说法:
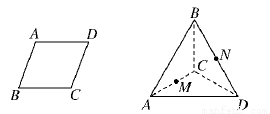
①AC⊥MN;
②DM与平面ABC所成的角是θ;
③线段MN的最大值是,最小值是;
④当θ=时,BC与AD所成的角等于.
其中正确的说法有 (填上所有正确说法的序号).
查看答案和解析>>
科目:高中数学 来源:2012-2013学年浙江省高三高考模拟测试理科数学试卷(解析版) 题型:选择题
如图,函数y=f(x)的图象为折线ABC,设f 1 (x)=f(x),f n+1 (x)=f [f n(x)],n∈N*,则函数y=f 4 (x)的图象为


A B C D
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com