
【题目】已知函数![]() 对任意实数
对任意实数![]() 均有
均有![]() ,其中常数
,其中常数![]() 为负数,且
为负数,且![]() 在区间
在区间![]() 上有表达式
上有表达式![]() .
.
(1)写出![]() 在
在![]() 上的表达式,并写出函数
上的表达式,并写出函数![]() 在
在![]() 上的单调区间(不用过程,直接写出即可);
上的单调区间(不用过程,直接写出即可);
(2)求出![]() 在
在![]() 上的最小值与最大值,并求出相应的自变量的取值.
上的最小值与最大值,并求出相应的自变量的取值.
【答案】(1) 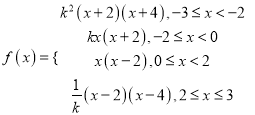 ,
, ![]() 和
和![]() 为增区间,
为增区间, ![]() 为减区间.
为减区间.
(2) ![]() ,
, ![]() .
.
【解析】试题分析:(1)根据函数关系,可求得![]() ,根据函数的定义域可分
,根据函数的定义域可分![]() 四段得到函数的解析式;根据分段函数的图像可求得函数的单调区间;(2)根据(1)函数的单调区间可知函数的最大值出自
四段得到函数的解析式;根据分段函数的图像可求得函数的单调区间;(2)根据(1)函数的单调区间可知函数的最大值出自![]() ,最小值出自
,最小值出自![]() ,再根据
,再根据![]() 的范围讨论最后的最大值和最小值.
的范围讨论最后的最大值和最小值.
试题解析:解:∵![]() ,∴
,∴![]() ,
,
∴![]() .
.
(1)当![]() 时,
时, ![]() ,
,
![]() ,
,
当![]() 时,
时, ![]() ,
,
![]() ,
,
当![]() 时,
时, ![]() ,
,
![]() ,
,
综上: ![]() 在
在![]() 上的表达式为
上的表达式为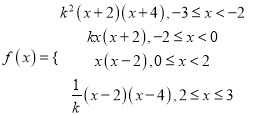 ,
,
由于![]() ,由
,由![]() 在
在![]() 上的图象,可得
上的图象,可得![]() 和
和![]() 为增区间,
为增区间, ![]() 为减区间.
为减区间.
(2)由(1)得![]() 的最小值出自
的最小值出自![]() ,
, ![]() ,
,
![]() 的最大值出自
的最大值出自![]() ,
, ![]() .
.
A.当![]() 时,
时, ![]() ,
, ![]() ,此时,
,此时, ![]() 最大值为
最大值为![]() ,最小值为
,最小值为![]() ;
;
B.当![]() 时,
时, ![]() ,
, ![]() ,此时
,此时![]() 最大值为1,最小值为
最大值为1,最小值为![]() ;
;
C.当![]() 时,
时, ![]() ,
, ![]() ;
;
此时: ![]() ,
, ![]() .
.


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】某家庭进行理财投资,根据长期收益率市场预测,投资![]() 类产品的收益与投资额成正比,投资
类产品的收益与投资额成正比,投资![]() 类产品的收益与投资额的算术平方根成正比.已知投资1万元时
类产品的收益与投资额的算术平方根成正比.已知投资1万元时![]() 两类产品的收益分别为0.125万元和0.5万元.
两类产品的收益分别为0.125万元和0.5万元.
(1)分别写出![]() 两类产品的收益与投资额的函数关系;
两类产品的收益与投资额的函数关系;
(2)该家庭有20万元资金,全部用于理财投资,问:怎么分配资金能使投资获得最大收益,其最大收益是多少万元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A(﹣1,1,2)、B(1,0,﹣1),设D在直线AB上,且 ![]() =2
=2 ![]() ,设C(λ,
,设C(λ, ![]() +λ,1+λ),若CD⊥AB,则λ的值为( )
+λ,1+λ),若CD⊥AB,则λ的值为( )
A.![]()
B.﹣ ![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某化工厂拟建一个下部为圆柱,上部为半球的容器(如图,圆柱高为h,半径为r,不计厚度,单位:米),按计划容积为72π立方米,且h≥2r,假设其建造费用仅与表面积有关(圆柱底部不计),已知圆柱部分每平方米的费用为2千元,半球部分每平方米4千元,设该容器的建造费用为y千元.
(Ⅰ)求y关于r的函数关系,并求其定义域;
(Ⅱ)求建造费用最小时的r.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂某种产品的年固定成本为250万元,每生产![]() 件,需另投入成本
件,需另投入成本![]() ,当年产量不足80件时,
,当年产量不足80件时, ![]() (万元),当年产量不少于80件时
(万元),当年产量不少于80件时![]() (万元),每件商品售价50万元,通过市场分析,该厂生产的商品能全部售完.
(万元),每件商品售价50万元,通过市场分析,该厂生产的商品能全部售完.
(1)写出年利润![]() (万元)关于年产量
(万元)关于年产量![]() (件)的函数解析式;
(件)的函数解析式;
(2)年产量为多少件时,该厂在这一商品的生产中所获利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示的四边形ABCD,已知 ![]() =(6,1),
=(6,1), ![]() =(x,y),
=(x,y), ![]() =(﹣2,﹣3)
=(﹣2,﹣3)
(1)若 ![]() 且﹣2≤x<1,求函数y=f(x)的值域;
且﹣2≤x<1,求函数y=f(x)的值域;
(2)若 ![]() 且
且 ![]() ,求x,y的值及四边形ABCD的面积.
,求x,y的值及四边形ABCD的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin2x﹣ ![]() sinxcosx+
sinxcosx+ ![]() ,g(x)=mcos(x+
,g(x)=mcos(x+ ![]() )﹣m+2
)﹣m+2
(1)若对任意的x1 , x2∈[0,π],均有f(x1)≥g(x2),求m的取值范围;
(2)若对任意的x∈[0,π],均有f(x)≥g(x),求m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com