
已知函数y=3sin(![]() x-
x-![]() ).
).
(1)用“五点法”作函数的图象;
(2)说出此图象是由y=sinx的图象经过怎样的变化得到的;
(3)求此函数的周期、振幅、初相;
(4)求此函数的对称轴、对称中心、单调递增区间.
(1)同解析;(2)同解析;(3)周期T=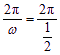 =4π,振幅A=3,初相是-
=4π,振幅A=3,初相是-![]() ;(4)所有图象与x轴的交点都是函数的对称中心,所以对称中心为点(
;(4)所有图象与x轴的交点都是函数的对称中心,所以对称中心为点(![]() +2kπ,0),k∈Z;[-
+2kπ,0),k∈Z;[-![]() +4kπ,
+4kπ,![]() +4kπ],k∈Z为此函数的单调递增区间;
+4kπ],k∈Z为此函数的单调递增区间;
(1)
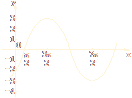
(2) “先平移,后伸缩”.
先把y=sinx的图象上所有的点向右平移![]() 个单位,得到y=sin(x-
个单位,得到y=sin(x-![]() )的图象;再把y=sin(x-
)的图象;再把y=sin(x-![]() )图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),得到y=sin(
)图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),得到y=sin(![]() x-
x-![]() )的图象;最后将y=sin(
)的图象;最后将y=sin(![]() x-
x-![]() )的图象上所有点的纵坐标伸长到原来的3倍(横坐标不变),就得到y=3sin(
)的图象上所有点的纵坐标伸长到原来的3倍(横坐标不变),就得到y=3sin(![]() x-
x-![]() )的图象.
)的图象.
(3)周期T=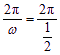 =4π,振幅A=3,初相是-
=4π,振幅A=3,初相是-![]() .
.
(4)由于y=3sin(![]() x-
x-![]() )是周期函数,通过观察图象可知,所有与x轴垂直并且通过图象的最值点的直线都是此函数的对称轴,即令
)是周期函数,通过观察图象可知,所有与x轴垂直并且通过图象的最值点的直线都是此函数的对称轴,即令![]() x-
x-![]() =
=![]() +kπ,解得直线方程为x=
+kπ,解得直线方程为x=![]() +2kπ,k∈Z;
+2kπ,k∈Z;
所有图象与x轴的交点都是函数的对称中心,所以对称中心为点(![]() +2kπ,0),k∈Z;
+2kπ,0),k∈Z;
x前的系数为正数,所以把![]() x-
x-![]() 视为一个整体,令-
视为一个整体,令-![]() +2kπ≤
+2kπ≤![]() x-
x-![]() ≤
≤![]() +2kπ,解得[-
+2kπ,解得[-![]() +4kπ,
+4kπ,![]() +4kπ],k∈Z为此函数的单调递增区间.
+4kπ],k∈Z为此函数的单调递增区间.


科目:高中数学 来源: 题型:
 已知函数y=3sin(
已知函数y=3sin(| 1 |
| 2 |
| π |
| 4 |
| x | |||||||||
(
|
|||||||||
3sin (
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| π |
| 2 |
| π |
| 8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com