
【题目】已知椭圆的右焦点F(m,0),左、右准线分别为l1:x=﹣m﹣1,l2:x=m+1,且l1 , l2分别与直线y=x相交于A,B两点.
(1)若离心率为 ![]() ,求椭圆的方程;
,求椭圆的方程;
(2)当 ![]()
![]() <7时,求椭圆离心率的取值范围.
<7时,求椭圆离心率的取值范围.
【答案】
(1)解:椭圆的右焦点F(m,0),故焦点在x轴上,设椭圆方程为: ![]() (a>b>0),
(a>b>0),
∴c=m,准线方程为:x= ![]() =m+1,
=m+1,
∴a2=m(m+1),b2=m …2分
由e= ![]() =
= ![]() =
= ![]() ,可得b=c,从而m=1,
,可得b=c,从而m=1,
故a= ![]() ,b=1,
,b=1,
∴椭圆方程: ![]() ;
;
(2)解:由题意可知:A(﹣m﹣1,﹣m﹣1),B(m+1,m+1),
∴ ![]() =(2m+1,m+1),
=(2m+1,m+1), ![]() =(1,m+1),
=(1,m+1),
故 ![]()
![]() =2m+1+(m+1)2=m2+4m+2<7,
=2m+1+(m+1)2=m2+4m+2<7,
解得:0<m<1,…12分
由离心率e= ![]() =
= ![]() =
= ![]() ,
,
故所求的离心率范围为(0, ![]() ).
).
【解析】(1)由题意可知: ![]() (a>b>0),由准线方程为:x=
(a>b>0),由准线方程为:x= ![]() =m+1,即可求得a2=m(m+1),b2=m,由e=
=m+1,即可求得a2=m(m+1),b2=m,由e= ![]() =
= ![]() =
= ![]() ,即可求得b=c,求得m的值,代入求得a和b的值,即可求得椭圆方程;(2)A(﹣m﹣1,﹣m﹣1),B(m+1,m+1),求得
,即可求得b=c,求得m的值,代入求得a和b的值,即可求得椭圆方程;(2)A(﹣m﹣1,﹣m﹣1),B(m+1,m+1),求得 ![]() =(2m+1,m+1),
=(2m+1,m+1), ![]() =(1,m+1),由
=(1,m+1),由 ![]()
![]() =m2+4m+2<7,即可求得0<m<1,由离心率e=
=m2+4m+2<7,即可求得0<m<1,由离心率e= ![]() =
= ![]() =
= ![]() ,即可求得椭圆离心率的取值范围.
,即可求得椭圆离心率的取值范围.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知![]() 是双曲线
是双曲线![]() 的左右焦点,以
的左右焦点,以![]() 为直径的圆与双曲线的一条渐近线交于点
为直径的圆与双曲线的一条渐近线交于点![]() ,与双曲线交于点
,与双曲线交于点![]() ,且
,且![]() 均在第一象限,当直线
均在第一象限,当直线![]() 时,双曲线的离心率为
时,双曲线的离心率为![]() ,若函数
,若函数![]() ,则
,则![]() ()
()
A. 1 B. ![]() C. 2 D.
C. 2 D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]()
(1)若直线![]() 与曲线
与曲线![]() 都只有两个交点,证明:这四个交点可以构成一个平行四边形,并计算该平行四边形的面积;
都只有两个交点,证明:这四个交点可以构成一个平行四边形,并计算该平行四边形的面积;
(2)设函数![]() 在[1,2]上的值域为
在[1,2]上的值域为![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 在椭圆
在椭圆![]() :
: ![]() (
(![]() )上,设
)上,设![]() ,
, ![]() ,
, ![]() 分别为左顶点、上顶点、下顶点,且下顶点
分别为左顶点、上顶点、下顶点,且下顶点![]() 到直线
到直线![]() 的距离为
的距离为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设点![]() ,
, ![]() (
(![]() )为椭圆
)为椭圆![]() 上两点,且满足
上两点,且满足![]() ,求证:
,求证: ![]() 的面积为定值,并求出该定值.
的面积为定值,并求出该定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】南京市江北新区计划在一个竖直长度为20米的瀑布![]() 正前方修建一座观光电梯
正前方修建一座观光电梯![]() 。如图所示,瀑布底部
。如图所示,瀑布底部![]() 距离水平地面的高度
距离水平地面的高度![]() 为60米,电梯上设有一个安全拍照口
为60米,电梯上设有一个安全拍照口![]() ,
, ![]() 上升的最大高度为60米。设
上升的最大高度为60米。设![]() 距离水平地面的高度为
距离水平地面的高度为![]() 米,
米, ![]() 处拍照瀑布的视角
处拍照瀑布的视角![]() 为
为![]() 。摄影爱好者发现,要使照片清晰,视角
。摄影爱好者发现,要使照片清晰,视角![]() 不能小于
不能小于![]() 。
。
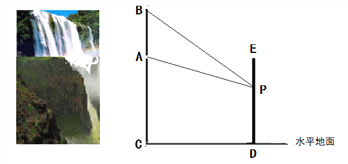
(1)当![]() 米时,视角
米时,视角![]() 恰好为
恰好为![]() ,求电梯和山脚的水平距离
,求电梯和山脚的水平距离![]() 。
。
(2)要使电梯拍照口![]() 的高度
的高度![]() 在52米及以上时,拍出的照片均清晰,请求出电梯和山脚的水平距离
在52米及以上时,拍出的照片均清晰,请求出电梯和山脚的水平距离![]() 的取值范围。
的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A、B、C为△ABC的三个内角,且其对边分别为a、b、c,若cosBcosC﹣sinBsinC= ![]() .
.
(1)求角A;
(2)若a=2 ![]() ,b+c=4,求△ABC的面积.
,b+c=4,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC的三个内角A,B,C所对的边分别为a,b,c,∠A是锐角,且 ![]() b=2asinB.
b=2asinB.
(1)求∠A的度数;
(2)若a=7,△ABC的面积为10 ![]() ,求b2+c2的值.
,求b2+c2的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com