练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    解答题

    若函数的单调递减区间是[－1，2]

    ①求b，c；②求[－3，4]上的最大值．

    答案：
    解析：

    　　解：(1)－－－－－－－－－－－－－－－－－－－－－－2分

    根据题意的解集为[－1，2]，－－－－－－－－－－－－－－－－－－3分

    即，－1，2是方程的解

    根据韦达定理所以－－－－－－－－6分

    　　(2)由(1)知道

    已知＝0－－－－－－－－－－－－－－－－－7分

    在区间上的根为－1，2，把－3，－1，2，4代入函数

    －－－－－－－－－－－－10分

    所以，的最大值为17－－－－－－－－－－－－－12分

    说明：利用列表说明函数单调性．来求最大值的得相应分数(5分)


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2004全国各省市高考模拟试题汇编(天利38套)·数学 题型：044

    设函数f(x)＝ax2＋bx＋1(a、b∈R)

    (1)若f(－1)＝0，则对任意实数均有f(x)≥0成立，求f(x)的表达式．

    (2)(文)在(1)的条件下，当x∈[－2，2]时，g(x)＝f(x)－kx是单调函数，求实数k的取值范围．

    (理)在(1)的条件下，当x∈[－2，2]时，g(x)＝xf(x)－kx是单调递增，求实数k的取值范围．

    查看答案和解析>>

    科目：高中数学 来源：2004全国各省市高考模拟试题汇编(天利38套)·数学 题型：044

    对于函数y＝f(x)(x∈D，D是此函数的定义域)若同时满足下列条件：

    (Ⅰ)f(x)在D内单调递增或单调递减；

    (Ⅱ)存在区间[a，b]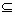D，使f(x)在[a，b]上的值域为[a，b]；那么，把y＝f(x)(x∈D)叫闭函数．

    (1)求闭函数y＝－x3符合条件(Ⅱ)的区间[a，b]；

    (2)判断函数f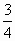(x)＝x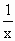＋(x∈R+)是否为闭函数？并说明理由；

    (3)若y＝k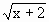＋是闭函数，求实数k的取值范围．

    查看答案和解析>>

    科目：高中数学 来源：成功之路·突破重点线·数学（学生用书） 题型：044

    设函数f(x)＝ax2＋bx＋1(a、b∈R)

    (1)若f(－1)＝0，则对任意实数均有f(x)≥0成立，求f(x)的表达式．

    (2)在(1)条件下，当x∈[－2，2]，g(x)＝xf(x)－kx单调递增，求实数k的取值范围．

    查看答案和解析>>

    科目：高中数学 来源：2010-2011学年河北省石家庄市毕业班复习质量检测数学理卷 题型：解答题

    三、解答题：本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤.

    17.(本小题满分10分）

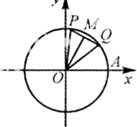
    如图，P，Q是以原点为圆心的单位圆上的两个动点,若它们同时从点A(1,0)出发，沿逆时针方向作匀角速度运动,其角速度分别为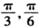（单位：弧度/秒）,M为线段PQ的中点，记经过x秒后(其中),

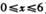    (I)求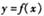的函数解析式；

     (II)将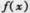图象上的各点均向右平移2个单位长度，得到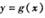的图象，求函数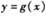的单调递减区间.

     

    查看答案和解析>>

    同步练习册答案