练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知函数．

    （Ⅰ）方程在区间上实数解的个数是__________；

    （Ⅱ）对于下列命题：① 函数是周期函数；

    ② 函数既有最大值又有最小值；

    ③ 函数的定义域是R，且其图象有对称轴；

    ④对于任意（是函数的导函数）．

    其中真命题的序号是           ．（填写出所有真命题的序号）

    （Ⅰ）   （Ⅱ）②③


    解析:

    （Ⅰ）由于，故

    在中的整数个数

    故在区间上实数解的个数为．

    （Ⅱ）命题①：由分母为，易知不是周期函数，故为假命题；

    命题②：由于是上的连续函数，且，可知既有最大值又有最小值，故为真命题；

    命题③：由于，故的定义域是R

    看到的对称轴为，且为的一条对称轴

    故为图象的对称轴，故为真命题；

    命题④：由在定义域R上连续，且，可知不可能在上为减函数，故为假命题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    精英家教网给出下列四个命题：
    ①已知函数y=2sin（x+φ）（0＜φ＜π）的图象如图所示，则?=
    π
    6
    或
    5
    6
    π    ；
    ②已知O、A、B、C是平面内不同的四点，且
    OA
    =α
    OB
    +β
    OC
    ，则α+β=1是A、B、C三点共线的充要条件；
    ③若数列an恒满足
    a
    2
    n+1
    a
    2
    n
    =p    （p为正常数，n∈N*），则称数列an是“等方比数列”．根据此定义可以断定：若数列an是“等方比数列”，则它一定是等比数列；
    ④求解关于变量m、n的不定方程3n-2=2m-1（n，m∈N*），可以得到该方程中变量n的所有取值的表达式为n=
    1
    12
    (4k+8)
    （k∈N*）．
    其中正确命题的序号是
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    下面四个命题：
    ①已知函数f(x)=
    		x
     ，x≥0 
    		-x
     ，x＜0 
    且f（a）+f（4）=4，那么a=-4；
    ②一组数据18，21，19，a，22的平均数是20，那么这组数据的方差是2；
    ③已知奇函数f（x）在（0，+∞）为增函数，且f（-1）=0，则不等式f（x）＜0的解集{x|x＜-1}；
    ④在极坐标系中，圆ρ=-4cosθ的圆心的直角坐标是（-2，0）．
    其中正确的是
    ②，④
    ②，④
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    下面四个命题：
    ①已知函数f(x)=
    		x
     ，x≥0 
    		-x
     ，x＜0 
    且f（a）+f（4）=4，那么a=-4；
    ②一组数据18，21，19，a，22的平均数是20，那么这组数据的方差是2；
    ③要得到函数y=sin(2x+
    π
    3
    )    的图象，只要将y=sin2x的图象向左平移
    π
    3
    单位；
    ④已知奇函数f（x）在（0，+∞）为增函数，且f（-1）=0，则不等式f（x）＜0的解集{x|x＜-1}．
    其中正确的是
    ②
    ②
    ．

    查看答案和解析>>

    科目：高中数学 来源：2010-2011学年安徽省六安一中高三（下）第七次月考数学试卷（理科）（解析版） 题型：填空题

    给出下列四个命题：
    ①已知函数y=2sin（x+φ）（0＜φ＜π）的图象如图所示，则；
    ②已知O、A、B、C是平面内不同的四点，且，则α+β=1是A、B、C三点共线的充要条件；
    ③若数列an恒满足（p为正常数，n∈N*），则称数列an是“等方比数列”．根据此定义可以断定：若数列an是“等方比数列”，则它一定是等比数列；
    ④求解关于变量m、n的不定方程3n-2=2m-1（n，m∈N*），可以得到该方程中变量n的所有取值的表达式为
    （k∈N*）．
    其中正确命题的序号是    ．

    查看答案和解析>>

    科目：高中数学 来源：2012-2013学年北京市高三阶段考试（二）文科数学试卷（解析版） 题型：填空题

    下面四个命题：

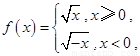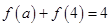    ①已知函数 且，那么；

    ②一组数据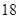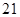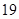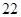，，，，的平均数是，那么这组数据的方差是；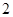

    ③要得到函数的图象，只要将的图象向左平移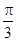单位；

    ④已知奇函数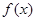在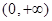为增函数，且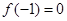，则不等式的解集为.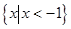

    其中正确的是__________________.

     

    查看答案和解析>>

    同步练习册答案