练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】某几何体被一平面所截后剩下几何体的三视图如图所示，则该剩下几何体的体积为（ ）

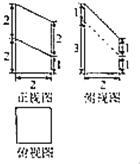
    A. 10B. 15C. 20D. 25

    【答案】A

    【解析】

    由三视图得到几何体的直观图，然后再结合图中的数据求出几何体的体积即可．

    由三视图可知该剩下几何体是由底面是边长为2的正方形、高为4的长方体截取得到的，为如图所示的几何体，其中底面是边长为2的正方形，四条侧棱长分别为4，3，2，1．

    方法一：由三视图可知，

    因为四边形是平面截原几何体所得的截面，

    所以为平行四边形．

    设，交于点，，交于点，

    则可得既为梯形的中位线，也为梯形的中位线，且．

    将所剩的几何体补成底面是边长为2的正方形、高为的长方体，

    则所求的几何体的体积为．

    故选A．

    方法二：由题意得，所剩几何体的体积为

    ．

    故选A．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数，.

    （1）讨论函数的单调性；

    （2）若存在与函数，的图象都相切的直线，求实数的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图所示的几何体，是将高为2、底面半径为1的圆柱沿过旋转轴的平面切开后，将其中一半沿切面向右水平平移后形成的封闭体.分别为的中点，为弧的中点，为弧的中点.

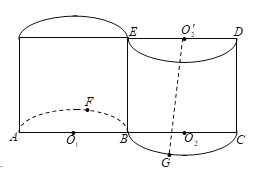
    （1）求直线与底面所成的角的大小；

    （2）求异面直线与所成的角的大小（结果用反三角函数值表示）.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为有效促进我市体育产业和旅游产业有机融合，提高我市的知名度，更好地宣传萍乡武功山，并通过赛事向社会各界传播健康、低碳、绿色、环保的运动理念。在今年9月21日第九届环鄱阳湖国际自行车大赛第九站比赛在我市武功山举行。在这次89.5公里的自行车个人赛中，其中25名参赛选手的成绩（单位：分钟）的茎叶图如图所示：

    （1）现将参赛选手按成绩由好到差编为1～25号，再用系统抽样方法从中选取5人，已知选手甲的成绩为145分钟，若甲被选取，求被选取的其余4名选手的成绩的平均数；

    （2）若从总体中选取一个样本，使得该样本的平均水平与总体相同，且样本的方差不大于7，则称选取的样本具有集中代表性，试从总体（25名参赛选手的成绩）选取一个具有集中代表性且样本容量为5的样本，并求该样本的方差．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】我国古代著名的周髀算经中提到：凡八节二十四气，气损益九寸九分六分分之一；冬至晷长一丈三尺五寸，夏至晷长一尺六寸意思是：一年有二十四个节气，每相邻两个节气之间的日影长度差为分；且“冬至”时日影长度最大，为1350分；“夏至”时日影长度最小，为160分则“立春”时日影长度为　　

    A. 分B. 分C. 分D. 分

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，三棱锥中，是的中点，为正三角形，，，，平面平面.

    （1）求证：；

    （2）求直线与平面所成角的正弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆C：（）的左、右焦点分别为，，离心率，点在椭圆C上，直线l过交椭圆于A，B两点.

    （1）求椭圆C的标准方程；

    （2）当时，点A在x轴上方时，求点A，B的坐标；

    （3）若直线交y轴于点M，直线交y轴于点N，是否存在直线l，使得与的面积满足，若存在，求出直线l的方程；若不存在，请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆C：=1（a＞b＞0）的离心率为，其内接正方形的面积为4．

    （Ⅰ）求椭圆C的标准方程；

    （Ⅱ）设M为椭圆C的右顶点，过点且斜率不为0的直线l与椭圆C相交于P，Q两点，记直线PM，QM的斜率分别为k1，k2，求证：k1k2为定值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某超市开展年终大回馈，设计了两种答题游戏方案：

    方案一：顾客先回答一道多选题，从第二道开始都回答单选题；

    方案二：顾客全部选择单选题进行回答；

    其中每道单选题答对得2分，每道多选题答对得3分，无论单选题还是多选题答错都得0分，每名参与的顾客至多答题3道.在答题过程中得到3分或3分以上立刻停止答题，并获得超市回馈的赠品.

    为了调查顾客对方案的选择情况，研究人员调查了参与游戏的500名顾客，所得结果如下表所示：

    14

    0

    1

    2

    3

    5

    6

    6

    6

    6

    8

    9

    15

    0

    2

    3

    4

    5

    5

    5

    7

    9

    16

    0

    0

    5

    6

    7

    男性

    女性

    选择方案一

    150

    80

    选择方案二

    150

    120

    （1）是否有95%的把握认为方案的选择与性别有关？

    （2）小明回答每道单选题的正确率为0.8，多选题的正确率为0.75,.

    ①若小明选择方案一，记小明的得分为，求的分布列及期望；

    ②如果你是小明，你觉得选择哪种方案更有可能获得赠品，请通过计算说明理由.

    附：，

    0.15

    0.10

    0.05

    0.025

    0.010

    0.005

    0.001

    2.072

    2.706

    3.841

    5.024

    6.635

    7.879

    10.828

    查看答案和解析>>

    同步练习册答案