
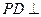 平面
平面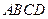 ,
,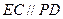 ,且
,且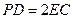 ,
, 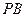 的中点,求证:
的中点,求证: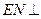 平面
平面 ;
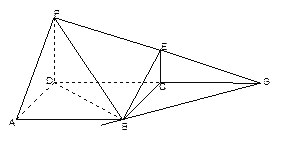
;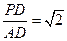 ,求平面PBE与平面ABCD所成的锐二面角的大小.
,求平面PBE与平面ABCD所成的锐二面角的大小.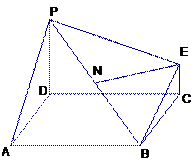
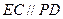 ,
, 平面
平面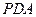 ,
,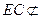 平面
平面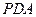
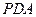 ,同理可得BC//平面
,同理可得BC//平面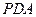 ----------------------------------------2分
----------------------------------------2分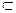 平面EBC,BC
平面EBC,BC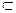 平面EBC且
平面EBC且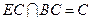
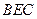 //平面
//平面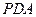 -----------------------------------------------------------------3分
-----------------------------------------------------------------3分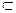 平面EBC ∴BE//平面PDA-----------------------------------------------------4分
平面EBC ∴BE//平面PDA-----------------------------------------------------4分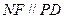 且
且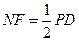 ,--------------------------6分
,--------------------------6分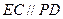 且
且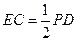
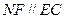 且
且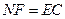
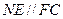

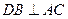 ,
,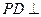 平面
平面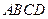 ,
,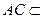 面
面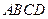 ∴
∴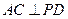 ,
,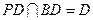
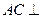 面
面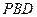 ∴
∴ 面
面 ----------------------------------------9分
----------------------------------------9分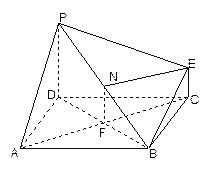
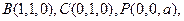
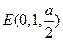 ,
,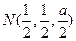 --------------------------------6分
--------------------------------6分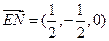 ,
,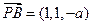 ,
,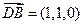
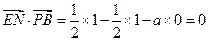 ,
, ,
,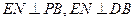 ---------------------------------8分
---------------------------------8分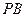 、
、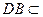 面
面 ,且
,且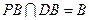
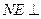 面
面 --------------------------------------------------------------------9分
--------------------------------------------------------------------9分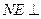 面
面
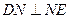 , ∵
, ∵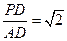 ,
,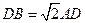 ∴
∴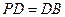 ∴
∴
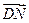 为平面PBE的法向量,设
为平面PBE的法向量,设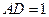 ,则
,则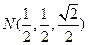 ∴
∴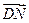 =
=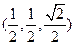 ---11分
---11分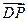 为平面ABCD的法向量,
为平面ABCD的法向量,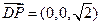 ,---------------------------------------------12分
,---------------------------------------------12分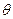 ,
,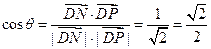 ------------------------------------------------13分
------------------------------------------------13分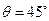 即平面PBE与平面ABCD所成的二面角为45°--------------------14分
即平面PBE与平面ABCD所成的二面角为45°--------------------14分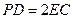 ∴
∴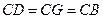
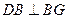 -------------------11分
-------------------11分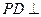 平面
平面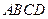 ,
,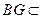 面
面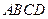
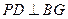 且
且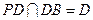
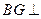 面
面 ∵
∵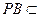 面
面
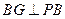
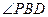 为平面PBE与平面ABCD所成的二面角的平面角----------------------------13分
为平面PBE与平面ABCD所成的二面角的平面角----------------------------13分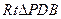 中 ∵
中 ∵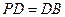
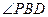 =45°即平面PBE与平面ABCD所成的二面角为45°----------------14分
=45°即平面PBE与平面ABCD所成的二面角为45°----------------14分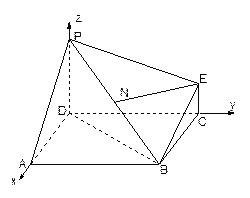


 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:高中数学 来源:不详 题型:解答题
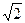 ,CD=1
,CD=1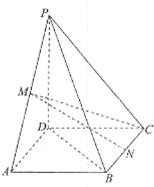
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
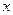
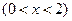 的小正方形,剰余部分围成一个长方体,该长方体的高是小正方形的边长.
的小正方形,剰余部分围成一个长方体,该长方体的高是小正方形的边长.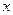 表示);
表示);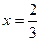 时,Vl取最大值
时,Vl取最大值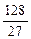 ,为了材料浪费最少,工人师傅还实践出了其它焊接方法,请写出与(1)的焊接方法更佳(使材料浪费最少,容积比Vl大)的设计方案,并计算利用你的设计方案所得到的容器的容积。
,为了材料浪费最少,工人师傅还实践出了其它焊接方法,请写出与(1)的焊接方法更佳(使材料浪费最少,容积比Vl大)的设计方案,并计算利用你的设计方案所得到的容器的容积。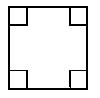
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com