
如图,在三棱锥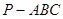 中,
中,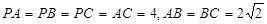

(1)求证:平面 ⊥平面
⊥平面
(2)求直线PA与平面PBC所成角的正弦值;
(3)若动点M在底面三角形ABC上,二面角M-PA-C的余弦值为 ,求BM的最小值.
,求BM的最小值.
(1)见解析 (2) 直线PA与平面PBC所成角的正弦值为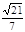 。 (3)
。 (3)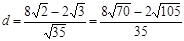 。
。
【解析】本试题主要是考查了面面垂直的证明,以及线面角的求解,以及二面角的大小的求解的综合运用。考查了同学们的空间想象能力和逻辑推理能力和计算能力的综合运用。
(1)利用线面垂直的判定定理,求证面面垂直的证明。
(2)建立空间直角坐标系,求解平面的法向量和直线的方向向量,利用数量积的性质得到线面角的求解。
(3)借助于上一问中的向量坐标,平面的法向量的法向量的夹角与二面角的平面角的大小相等或者互补
解:(1)取AC中点O,因为AP=BP,所以OP⊥OC 由已知易得三角形ABC为直角三角形,∴OA=OB=OC,⊿POA≌⊿POB≌⊿POC,∴OP⊥OB
∴OP⊥平面ABC, ∵OP在平面PAC中,∴平面 ⊥平面
⊥平面 4分
4分
(2) 以O为坐标原点,OB、OC、OP分别为x、y、z轴建立如图所示空间直角坐标系.

由已知得O(0,0,0),B(2,0,0),A(0,-2,0),C(0,2,0),P(0,0,
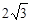 ),
5分
),
5分
∴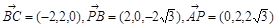 设平面PBC的法向量
设平面PBC的法向量 ,
,
由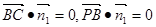 得方程组
得方程组
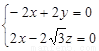 ,取
,取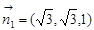 6分
6分
∴ 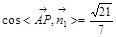 ∴直线PA与平面PBC所成角的正弦值为
∴直线PA与平面PBC所成角的正弦值为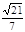 。 8分
。 8分
(2)由题意平面PAC的法向量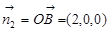 ,
,
设平面PAM的法向量为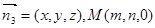
∵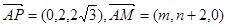 又因为
又因为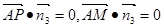
∴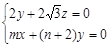 取
取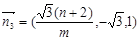
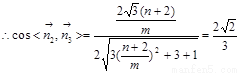
∴  ∴
∴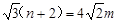 11分
11分
∴B点到AM的最小值为垂直距离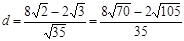 。
。


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2013届广西玉林市高二下学期三月月考文科数学试卷(解析版) 题型:解答题
如图,在三棱锥 中,侧面
中,侧面 与侧面
与侧面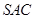 均为等边三角形,
均为等边三角形,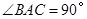 ,
,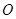 为
为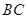 中点.
中点.
(Ⅰ)证明: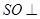 平面
平面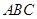 ;
;
(Ⅱ)求二面角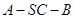 的余弦值. (本题12分)
的余弦值. (本题12分)

查看答案和解析>>
科目:高中数学 来源:2011-2012学年浙江省台州市高三上学期期末理科数学试卷 题型:解答题
如图,在三棱锥 中,
中, 两两垂直且相等,过
两两垂直且相等,过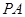 的中点
的中点 作平面
作平面 ∥
∥ ,且
,且 分别交
分别交 于
于 ,交
,交 的延长线于
的延长线于 .
.
(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)若 ,求二面角
,求二面角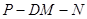 的余弦值.
的余弦值.

查看答案和解析>>
科目:高中数学 来源:2011---2012学年四川省高二10月考数学试卷 题型:解答题
如图:在三棱锥 中,已知点
中,已知点 、
、 、
、 分别为棱
分别为棱 、
、 、
、 的中点.
的中点.
(Ⅰ)求证: ∥平面
∥平面 ;
;
(Ⅱ)若 ,
, ,求证:平面
,求证:平面 ⊥平面
⊥平面 .
.

查看答案和解析>>
科目:高中数学 来源:黑龙江省2013届高一下学期期末考试数学(理) 题型:解答题
如图,在三棱锥 中,
中, ,
, 为
为 中点。(1)求证:
中点。(1)求证: 平面
平面
(2)在线段 上是否存在一点
上是否存在一点 ,使二面角
,使二面角 的平面角的余弦值为
的平面角的余弦值为 ?若存在,确定
?若存在,确定 点位置;若不存在,说明理由。
点位置;若不存在,说明理由。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com