解:(Ⅰ)设x
1,x
2∈[0,1],x
1<x
2,则x
2-x
1∈[0,1].
∴f(x
1)=f[(x
2-x
1)+x
1]≥f(x
2-x
1)+f(x
1)-2.
∴f(x
2)-f(x
1)≥f(x
2-x
1)-2≥0.∴f(x
1)≤f(x
2).
则当0≤x≤1时,f(0)≤f(x)≤f(1).
在③中,令x
1=x
2=0,得f(0)≤2,由②得f(0)≥2,∴f(0)=2.
∴当x=0时,f(x)取得最小值为2;
当x=1时,f(x)取得最大值为3.
(Ⅱ)在③中,令x
1=x
2=

,得
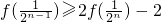
∴

则
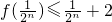
.
(Ⅲ)对x∈[0,1],总存在n∈N,满足

<x≤

.
由(Ⅰ)与(Ⅱ),得

,又2x+2>2•

+2=

+2.
∴f(x)<x+2.
综上所述,对任意x∈[0,1].f(x)<x+2恒成立.
分析:(Ⅰ)对于抽象函数的最值问题,可考虑此函数的单调性;
(Ⅱ)题中条件:f(x
1+x
2)≥f(x
1)+f(x
2)-2,令x
1=x
2=

,得
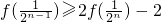
,
利用它进行放缩,可证得答案,
(Ⅲ)因为由题意可得:对x∈[0,1],总存在n∈N,满足

<x≤

.结合(I)、(II)可证得(III).
点评:本题考查了抽象函数,抽象函数是相对于给出具体解析式的函数来说的,它虽然没有具体的表达式,但是有一定的对应法则,满足一定的性质,这种对应法则及函数的相应的性质是解决问题的关键.抽象函数的抽象性赋予它丰富的内涵和多变的思维价值,可以考查类比猜测,合情推理的探究能力和创新精神.

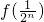 与
与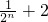 的大小;
的大小;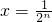 (n∈N)时,有f(x)<2x+2,由此他提出猜想:对一切x∈(0,1],都有f(x)<2x+2,请你判断此猜想是否正确,并说明理由.
(n∈N)时,有f(x)<2x+2,由此他提出猜想:对一切x∈(0,1],都有f(x)<2x+2,请你判断此猜想是否正确,并说明理由. ,得
,得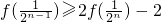

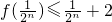 .
.  <x≤
<x≤ .
.  ,又2x+2>2•
,又2x+2>2• +2=
+2= +2.
+2. ,得
,得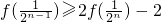 ,
, <x≤
<x≤ .结合(I)、(II)可证得(III).
.结合(I)、(II)可证得(III).

