
【题目】设函数![]() ,
,![]() ,其中
,其中![]() ,
,![]() 为正实数.
为正实数.
(1)若![]() 的图象总在函数
的图象总在函数![]() 的图象的下方,求实数
的图象的下方,求实数![]() 的取值范围;
的取值范围;
(2)设![]() ,证明:对任意
,证明:对任意![]() ,都有
,都有![]() .
.
【答案】(1)![]() (2)证明见解析
(2)证明见解析
【解析】
(1)据题意可得![]() 在区间
在区间![]() 上恒成立,利用导数讨论函数的单调性,从而求出满足不等式的
上恒成立,利用导数讨论函数的单调性,从而求出满足不等式的![]() 的取值范围;(2)不等式整理为
的取值范围;(2)不等式整理为![]() ,由(1)可知当
,由(1)可知当![]() 时,
时,![]() ,利用导数判断函数
,利用导数判断函数![]() 的单调性从而证明
的单调性从而证明![]() 在区间
在区间![]() 上成立,从而证明对任意
上成立,从而证明对任意![]() ,都有
,都有![]() .
.
(1)解:因为函数![]() 的图象恒在
的图象恒在![]() 的图象的下方,
的图象的下方,
所以![]() 在区间
在区间![]() 上恒成立.
上恒成立.
设![]() ,其中
,其中![]() ,
,
所以![]() ,其中
,其中![]() ,
,![]() .
.
①当![]() ,即
,即![]() 时,
时,![]() ,
,
所以函数![]() 在
在![]() 上单调递增,
上单调递增,![]() ,
,
故![]() 成立,满足题意.
成立,满足题意.
②当![]() ,即
,即![]() 时,设
时,设![]() ,
,
则![]() 图象的对称轴
图象的对称轴![]() ,
,![]() ,
,![]() ,
,
所以![]() 在
在![]() 上存在唯一实根,设为
上存在唯一实根,设为![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,
所以![]() 在
在![]() 上单调递减,此时
上单调递减,此时![]() ,不合题意.
,不合题意.
综上可得,实数![]() 的取值范围是
的取值范围是![]() .
.
(2)证明:由题意得![]()
![]() ,
,
因为当![]() 时,
时,![]() ,
,![]() ,
,
所以![]()
![]() .
.
令![]() ,则
,则![]() ,
,
所以![]() 在
在![]() 上单调递增,
上单调递增,![]() ,即
,即![]() ,
,
所以![]() ,从而
,从而![]() .
.
由(1)知当![]() 时,
时,![]() 在
在![]() 上恒成立,整理得
上恒成立,整理得![]() .
.
令![]() ,则要证
,则要证![]() ,只需证
,只需证![]() .
.
因为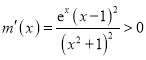 ,所以
,所以![]() 在
在![]() 上单调递增,
上单调递增,
所以![]() ,即
,即![]() 在
在![]() 上恒成立.
上恒成立.
综上可得,对任意![]() ,都有
,都有![]() 成立.
成立.


 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:高中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB//CD,∠ABD=30°,AB=2CD=2AD=2,DE⊥平面ABCD,EF//BD,且BD=2EF.
(Ⅰ)求证:平面ADE⊥平面BDEF;
(Ⅱ)若二面角C![]() BF
BF![]() D的大小为60°,求CF与平面ABCD所成角的正弦值.
D的大小为60°,求CF与平面ABCD所成角的正弦值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“初中数学靠练,高中数学靠悟”.总结反思自己已经成为数学学习中不可或缺的一部分,为了了解总结反思对学生数学成绩的影响,某校随机抽取200名学生,抽到不善于总结反思的学生概率是0.6.
(1)完成![]() 列联表(应适当写出计算过程);
列联表(应适当写出计算过程);
(2)试运用独立性检验的思想方法分析是否有![]() 的把握认为学生的学习成绩与善于总结反思有关.
的把握认为学生的学习成绩与善于总结反思有关.
统计数据如下表所示:
不善于总结反思 | 善于总结反思 | 合计 | |
学习成绩优秀 | 40 | ||
学习成绩一般 | 20 | ||
合计 | 200 |
参考公式:![]() 其中
其中![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某省新课改后某校为预测2020届高三毕业班的本科上线情况,从该校上一届高三(1)班到高三(5)班随机抽取50人,得到各班抽取的人数和其中本科上线人数,并将抽取数据制成下面的条形统计图.
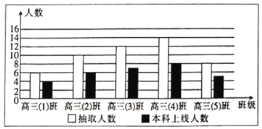
(1)根据条形统计图,估计本届高三学生本科上线率.
(2)已知该省甲市2020届高考考生人数为4万,假设以(1)中的本科上线率作为甲市每个考生本科上线的概率.
(i)若从甲市随机抽取10名高三学生,求恰有8名学生达到本科线的概率(结果精确到0.01);
(ii)已知该省乙市2020届高考考生人数为3.6万,假设该市每个考生本科上线率均为![]() ,若2020届高考本科上线人数乙市的均值不低于甲市,求p的取值范围.
,若2020届高考本科上线人数乙市的均值不低于甲市,求p的取值范围.
可能用到的参考数据:取![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,曲线![]() 是由两个定点
是由两个定点![]() 和点
和点![]() 的距离之积等于
的距离之积等于![]() 的所有点组成的,对于曲线
的所有点组成的,对于曲线![]() ,有下列四个结论:①曲线
,有下列四个结论:①曲线![]() 是轴对称图形;②曲线
是轴对称图形;②曲线![]() 上所有的点都在单位圆
上所有的点都在单位圆![]() 内;③曲线
内;③曲线![]() 是中心对称图形;④曲线
是中心对称图形;④曲线![]() 上所有点的纵坐标
上所有点的纵坐标![]() .其中,所有正确结论的序号是______.
.其中,所有正确结论的序号是______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知单调递增的等比数列![]() 满足:
满足:![]() .且
.且![]() 是
是![]() ,
,![]() 的等差中项.又数列
的等差中项.又数列![]() 满足:
满足:![]() ,
,![]() ,
,![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)若![]() ,且数列
,且数列![]() 为等比数列,求
为等比数列,求![]() 的值;
的值;
(3)若![]() ,且
,且![]() 为数列
为数列![]() 的最小项,求
的最小项,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】德国著名数学家狄利克雷(Dirichlet,1805~1859)在数学领域成就显著.19世纪,狄利克雷定义了一个“奇怪的函数” 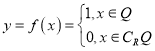 其中R为实数集,Q为有理数集.则关于函数
其中R为实数集,Q为有理数集.则关于函数![]() 有如下四个命题,正确的为( )
有如下四个命题,正确的为( )
A.函数![]() 是偶函数
是偶函数
B.![]() ,
,![]() ,
,![]() 恒成立
恒成立
C.任取一个不为零的有理数T,![]() 对任意的
对任意的![]() 恒成立
恒成立
D.不存在三个点![]() ,
,![]() ,
,![]() ,使得
,使得![]() 为等腰直角三角形
为等腰直角三角形
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于正整数![]() ,如果
,如果![]() 个整数
个整数![]() 满足
满足![]() ,
,
且![]() ,则称数组
,则称数组![]() 为
为![]() 的一个“正整数分拆”.记
的一个“正整数分拆”.记![]() 均为偶数的“正整数分拆”的个数为
均为偶数的“正整数分拆”的个数为![]() 均为奇数的“正整数分拆”的个数为
均为奇数的“正整数分拆”的个数为![]() .
.
(Ⅰ)写出整数4的所有“正整数分拆”;
(Ⅱ)对于给定的整数![]() ,设
,设![]() 是
是![]() 的一个“正整数分拆”,且
的一个“正整数分拆”,且![]() ,求
,求![]() 的最大值;
的最大值;
(Ⅲ)对所有的正整数![]() ,证明:
,证明:![]() ;并求出使得等号成立的
;并求出使得等号成立的![]() 的值.
的值.
(注:对于![]() 的两个“正整数分拆”
的两个“正整数分拆”![]() 与
与![]() ,当且仅当
,当且仅当![]() 且
且![]() 时,称这两个“正整数分拆”是相同的.)
时,称这两个“正整数分拆”是相同的.)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com