连续两次掷骰子,出现点数之和等于4的概率为 (结果用数值表示).
【答案】
分析:本题是一个古典概型,试验发生包含的事件总的试验结果为36个,满足条件的事件是点数和为的结果为4,可以列举出共3个,根据古典概型的概率公式得到结果.
解答:解:由题意知本题是一个古典概型,
试验发生包含的事件总的试验结果为36个,
满足条件的事件是点数和为的结果为4,
可以列举出(1,3),(2,2),(3,1)共3个,
由古典概型概率计算公式可得P=
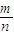
=
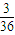
=
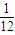
.
故答案为

.
点评:本题考查古典概型,考查分步计数问题,是一个基础题,解题过程中要用到列举法来做出事件所包含的事件数,注意列举时,做到不重不漏.
