
【题目】定义域是![]() 上的连续函数
上的连续函数![]() 图像的两个端点为
图像的两个端点为![]() 、
、![]() ,
,![]() 是图像
是图像![]() 上任意一点,过点
上任意一点,过点![]() 作垂直于
作垂直于![]() 轴的直线
轴的直线![]() 交线段
交线段![]() 于点
于点![]() (点
(点![]() 与点
与点![]() 可以重合),我们称
可以重合),我们称![]() 的最大值为该函数的“曲径”,下列定义域是
的最大值为该函数的“曲径”,下列定义域是![]() 上的函数中,曲径最小的是( )
上的函数中,曲径最小的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
【答案】D
【解析】
根据已知中函数的“曲径”的定义,逐一求出给定四个函数的曲径,比较后,可得答案.
当y=f(x)=sin![]() x时,端点A(1,
x时,端点A(1,![]() ),B(2,
),B(2,![]() ),直线AB的方程为y
),直线AB的方程为y![]() ,
,
故|![]() |=sin
|=sin![]() x
x![]() ,当x
,当x![]() 时,|
时,|![]() |的最大值为1
|的最大值为1![]() ,即该函数的“曲径”为1
,即该函数的“曲径”为1![]() ,
,
当y=f(x)=x2时,端点A(1,1),B(2,4),直线AB的方程为y=3x﹣2,
故|![]() |=3x﹣2﹣x2,当x
|=3x﹣2﹣x2,当x![]() 时,|
时,|![]() |的最大值为
|的最大值为![]() ,即该函数的“曲径”为
,即该函数的“曲径”为![]() ,
,
当y=f(x)![]() 时,端点A(1,2),B(2,1),直线AB的方程为y=﹣x+3,
时,端点A(1,2),B(2,1),直线AB的方程为y=﹣x+3,
故|![]() |=﹣x+3
|=﹣x+3![]() ,当x
,当x![]() 时,|
时,|![]() |的最大值为3﹣2
|的最大值为3﹣2![]() ,即该函数的“曲径”为3﹣2
,即该函数的“曲径”为3﹣2![]() ,
,
当y=f(x)=x![]() 时,端点A(1,0),B(2,
时,端点A(1,0),B(2,![]() ),直线AB的方程为y
),直线AB的方程为y![]() x
x![]() ,
,
故|![]() |=x
|=x![]() x
x![]() x
x![]() ,当x
,当x![]() 时,|
时,|![]() |的最大值为
|的最大值为![]() ,即该函数的“曲径”为
,即该函数的“曲径”为![]() ,
,
故函数y=x![]() 的曲径最小,
的曲径最小,
故选:D.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() 的定义域为
的定义域为![]() ,且
,且![]() 的图像连续不间断,若函数
的图像连续不间断,若函数![]() 满足:对于给定的实数
满足:对于给定的实数![]() 且
且![]() ,存在
,存在![]() ,使得
,使得![]() ,则称
,则称![]() 具有性质
具有性质![]() .
.
(1)已知函数![]() ,判断
,判断![]() 是否具有性质
是否具有性质![]() ,并说明理由;
,并说明理由;
(2)求证:任取![]() ,函数
,函数![]() ,
,![]() 具有性质
具有性质![]() ;
;
(3)已知函数![]() ,
,![]() ,若
,若![]() 具有性质
具有性质![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
袋中有形状和大小完全相同的四种不同颜色的小球,每种颜色的小球各有4个,分别编号为1,2,3,4.现从袋中随机取两个球.
(Ⅰ)若两个球颜色不同,求不同取法的种数;
(Ⅱ)在(1)的条件下,记两球编号的差的绝对值为随机变量X,求随机变量X的概率分布与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知变量![]() 、
、![]() 之间的线性回归方程为
之间的线性回归方程为![]() ,且变量
,且变量![]() 、
、![]() 之间的一-组相关数据如下表所示,则下列说法错误的是( )
之间的一-组相关数据如下表所示,则下列说法错误的是( )
|
|
|
|
|
|
|
|
|
|
A.可以预测,当![]() 时,
时,![]() B.
B.![]()
C.变量![]()
![]() 之间呈负相关关系D.该回归直线必过点
之间呈负相关关系D.该回归直线必过点![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“绿水青山就是金山银山”,“建设美丽中国”已成为新时代中国特色社会主义生态文明建设的重要内容,某班在一次研学旅行活动中,为了解某苗圃基地的柏树幼苗生长情况,在这些树苗中随机抽取了120株测量高度(单位:![]() ),经统计,树苗的高度均在区间
),经统计,树苗的高度均在区间![]() 内,将其按
内,将其按![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分成6组,制成如图所示的频率分布直方图.据当地柏树苗生长规律,高度不低于
分成6组,制成如图所示的频率分布直方图.据当地柏树苗生长规律,高度不低于![]() 的为优质树苗.
的为优质树苗.

(1)求图中![]() 的值;
的值;
(2)已知所抽取的这120株树苗来自于![]() ,
,![]() 两个试验区,部分数据如下列联表:
两个试验区,部分数据如下列联表:
|
| 合计 | |
优质树苗 | 20 | ||
非优质树苗 | 60 | ||
合计 |
将列联表补充完整,并判断是否有99.9%的把握认为优质树苗与![]() ,
,![]() 两个试验区有关系,并说明理由;
两个试验区有关系,并说明理由;
(3)通过用分层抽样方法从![]() 试验区被选中的树苗中抽取5株,若从这5株树苗中随机抽取2株,求优质树苗和非优质树苗各有1株的概率.
试验区被选中的树苗中抽取5株,若从这5株树苗中随机抽取2株,求优质树苗和非优质树苗各有1株的概率.
附:参考公式与参考数据:
其中![]()
| 0.010 | 0.005 | 0.001 |
| 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有一种密码,明文是由三个字符组成,密码是由明文对应的五个数字组成,编码规则如下表:明文由表中每一排取一个字符组成,且第一排取的字符放在第一位,第二排取的字符放在第二位,第三排取的字符放在第三位,对应的密码由明文对应的数字按相同的次序排成一排组成.
| 明文字符 | A | B | C | D |
密码字符 | 11 | 12 | 13 | 14 | |
| 明文字符 | E | F | G | H |
密码字符 | 21 | 22 | 23 | 24 | |
| 明文字符 | M | N | P | Q |
密码字符 | 1 | 2 | 3 | 4 |
设随机变量![]() 表示密码中不同数字的个数.
表示密码中不同数字的个数.
(Ⅰ)求![]() 的分布列和它的数学期望.
的分布列和它的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为美化校园,江苏省淮阴中学将一个半圆形的边角地改造为花园.如图所示,O为圆心,半径为1千米,点A、B、P都在半圆弧上,设∠NOP=∠POA=![]() ,∠AOB=
,∠AOB=![]() ,且
,且![]() .
.
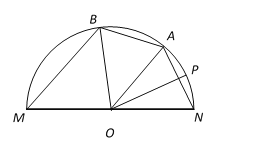
(1)请用![]() 分别表示线段NA、BM的长度;
分别表示线段NA、BM的长度;
(2)若在花园内铺设一条参观线路,由线段NA、AB、BM三部分组成,则当![]() 取何值时,参观线路最长?
取何值时,参观线路最长?
(3)若在花园内的扇形ONP和四边形OMBA内种满杜鹃花,则当![]() 取何值时,杜鹃花的种植总面积最大?
取何值时,杜鹃花的种植总面积最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com