
【题目】如图,![]() 垂直于
垂直于![]() 所在的平面
所在的平面![]() ,
,![]() 为
为![]() 的直径,
的直径,![]() 是弧
是弧![]() 上的一个动点(不与端点
上的一个动点(不与端点![]() 重合),
重合),![]() 为
为![]() 上一点,且
上一点,且![]() 是线段
是线段![]() 上的一个动点(不与端点
上的一个动点(不与端点![]() 重合).
重合).
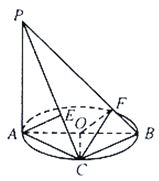
(1)求证:![]() 平面
平面![]() ;
;
(2)若![]() 是弧
是弧![]() 的中点,
的中点,![]() 是锐角,且三棱锥
是锐角,且三棱锥![]() 的体积为
的体积为![]() ,求
,求![]() 的值.
的值.
【答案】(1)见证明;(2)![]()
【解析】
(1)由![]() 为
为![]() 的直径,得到
的直径,得到![]() ,又由
,又由![]() 平面
平面![]() ,证得
,证得![]() ,利用线面垂直的判定定理得到
,利用线面垂直的判定定理得到![]() 平面
平面![]() ,再利用线面垂直的判定定理,即可证得
,再利用线面垂直的判定定理,即可证得![]() 平面
平面![]() .
.
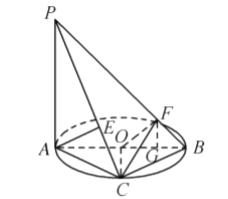
(2)当点![]() 位于线段
位于线段![]() 上时,如图所示:作
上时,如图所示:作![]() ,垂足为点
,垂足为点![]() ,根据线面垂直的判定定,证得
,根据线面垂直的判定定,证得![]() 平面
平面![]() ,得到
,得到![]() 是三棱锥
是三棱锥![]() 的底面
的底面![]() 上的高,再来体积公式,列出方程,即可求解.
上的高,再来体积公式,列出方程,即可求解.
(1)证明:因为![]() 为
为![]() 的直径,
的直径,
所以根据直径所对的圆周角是直角,可知![]() ,
,
因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() ,
,
又因为![]() 平面
平面![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,所以
,所以![]() ,
,
又因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
(2)当点![]() 位于线段
位于线段![]() 上时,如图所示:作
上时,如图所示:作![]() ,垂足为点
,垂足为点![]() ,
,
因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() ,
,
又因为![]() ,所以
,所以![]() ,
,
又因为![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,
,
所以![]() 是三棱锥
是三棱锥![]() 的底面
的底面![]() 上的高,
上的高,
因为![]() 是弧
是弧![]() 的中点,且
的中点,且![]() ,
,
所以![]() ,且
,且![]() ,
,
若三棱锥![]() 的体积为
的体积为![]() ,
,
则![]() ,解得
,解得![]() ,
,
所以![]() ,所以
,所以![]() ,
,
所以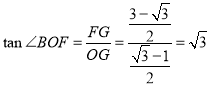 ,
,
综上所述,当三棱锥![]() 的体积为
的体积为![]() 时,
时,![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左焦点为F,点
的左焦点为F,点![]() ,过M的直线与椭圆E交于A,B两点,线段AB中点为C,设椭圆E在A,B两点处的切线相交于点P,O为坐标原点.
,过M的直线与椭圆E交于A,B两点,线段AB中点为C,设椭圆E在A,B两点处的切线相交于点P,O为坐标原点.
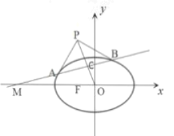
(1)证明:O、C、P三点共线;
(2)已知![]() 是抛物线
是抛物线![]() 的弦,所在直线过该抛物线的准线与y轴的交点,
的弦,所在直线过该抛物线的准线与y轴的交点,![]() 是弦
是弦![]() 在两端点处的切线的交点,小明同学猜想:
在两端点处的切线的交点,小明同学猜想:![]() 在定直线上.你认为小明猜想合理吗?若合理,请写出
在定直线上.你认为小明猜想合理吗?若合理,请写出![]() 所在直线方程;若不合理,请说明理由.
所在直线方程;若不合理,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年席卷全球的新冠肺炎给世界人民带来了巨大的灾难,面对新冠肺炎,早发现、早诊断、早隔离、早治疗是有效防控疾病蔓延的重要举措之一.某社区对![]() 位居民是否患有新冠肺炎疾病进行筛查,先到社区医务室进行口拭子核酸检测,检测结果成阳性者,再到医院做进一步检查,己知随机一人其口拭子核酸检测结果成阳性的概率为
位居民是否患有新冠肺炎疾病进行筛查,先到社区医务室进行口拭子核酸检测,检测结果成阳性者,再到医院做进一步检查,己知随机一人其口拭子核酸检测结果成阳性的概率为![]() %,且每个人的口拭子核酸是否呈阳性相互独立.
%,且每个人的口拭子核酸是否呈阳性相互独立.
(1)假设该疾病患病的概率是![]() %,且患病者口拭子核酸呈阳性的概率为
%,且患病者口拭子核酸呈阳性的概率为![]() %,设这
%,设这![]() 位居民中有一位的口拭子核酸检测呈阳性,求该居民可以确诊为新冠肺炎患者的概率;
位居民中有一位的口拭子核酸检测呈阳性,求该居民可以确诊为新冠肺炎患者的概率;
(2)根据经验,口拭子核酸检测采用分组检测法可有效减少工作量,具体操作如下:将![]() 位居民分成若干组,先取每组居民的口拭子核酸混在一起进行检测,若结果显示阴性,则可断定本组居民没有患病,不必再检测;若结果显示阳性,则说明本组中至少有一位居民患病,需再逐个进行检测,现有两个分组方案:
位居民分成若干组,先取每组居民的口拭子核酸混在一起进行检测,若结果显示阴性,则可断定本组居民没有患病,不必再检测;若结果显示阳性,则说明本组中至少有一位居民患病,需再逐个进行检测,现有两个分组方案:
方案一:将![]() 位居民分成
位居民分成![]() 组,每组
组,每组![]() 人;
人;
方案二:将![]() 位居民分成
位居民分成![]() 组,每组
组,每组![]() 人;
人;
试分析哪一个方案的工作量更少?
(参考数据:![]() ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的最小正周期为
的最小正周期为![]() ,其图象关于直线
,其图象关于直线![]() 对称.给出下面四个结论:①将
对称.给出下面四个结论:①将![]() 的图象向右平移
的图象向右平移![]() 个单位长度后得到函数图象关于原点对称;②点
个单位长度后得到函数图象关于原点对称;②点![]() 为
为![]() 图象的一个对称中心;③
图象的一个对称中心;③![]() ;④
;④![]() 在区间
在区间![]() 上单调递增.其中正确的结论为( )
上单调递增.其中正确的结论为( )
A.①②B.②③C.②④D.①④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A,B是椭圆C:![]() )的左右顶点,P点为椭圆C上一点,点P关于x轴的对称点为H,且
)的左右顶点,P点为椭圆C上一点,点P关于x轴的对称点为H,且![]()
(1)若椭圆C经过了圆![]() 的圆心,求椭圆C的标准方程;
的圆心,求椭圆C的标准方程;
(2)在(1)的条件下,抛物线D:![]() 的焦点F与点
的焦点F与点![]() 关于y轴上某点对称,且抛物线D与椭圆C在第四象限交于点Q,过点Q作直线与抛物线D有唯一公共点,求该直线与两坐标轴围成的三角形面积.
关于y轴上某点对称,且抛物线D与椭圆C在第四象限交于点Q,过点Q作直线与抛物线D有唯一公共点,求该直线与两坐标轴围成的三角形面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】手机运动计步已成为一种时尚,某中学统计了该校教职工一天行走步数(单位:百步),绘制出如下频率分布直方图:
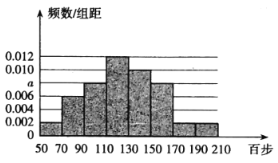
(Ⅰ)求直方图中![]() 的值,并由频率分布直方图估计该校教职工一天步行数的中位数;
的值,并由频率分布直方图估计该校教职工一天步行数的中位数;
(Ⅱ)若该校有教职工175人,试估计一天行走步数不大于130百步的人数;
(Ⅲ)在(Ⅱ)的条件下该校从行走步数大于150百步的3组教职工中用分层抽样的方法选取6人参加远足活动,再从6人中选取2人担任领队,求这两人均来自区间![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】抛物线C:y2=2px(p>0)的焦点为F,点P在C上,若PF⊥x轴,且△POF(O为坐标原点)的面积为1.
(1)求抛物线C的方程;
(2)若C上的两动点A,B(A,B在x轴异侧)满足![]() ,且|FA|+|FB|=|AB|+2,求|AB|的值.
,且|FA|+|FB|=|AB|+2,求|AB|的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={(x,y)|(x﹣3﹣4cosq)2+(y﹣5﹣4sinq)2=4,θ∈R},B={(x,y)|3x+4y﹣19=0}.记集合P=A∩B,则集合P所表示的轨迹的长度为( )
A.8![]() B.8
B.8![]() C.8
C.8![]() D.8
D.8![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,倾斜角为
中,倾斜角为![]() 的直线
的直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).在以坐标原点为极点,
为参数).在以坐标原点为极点,![]() 轴正半轴为极轴的极坐标系中,曲线
轴正半轴为极轴的极坐标系中,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点,且
两点,且![]() ,求直线
,求直线![]() 的倾斜角.
的倾斜角.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com