【答案】
分析:(1)利用二项式定理求出,a
1=1,d=1,①利用组合数公式可求出S
2,S
3,S
4,②可得出S
n=

b
n,再用倒序相加法证明.
(2)通项a
kC
nk=
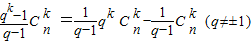
,利用分组法,结合二项式定理的逆用、二项式系数的性质,求出 T
n=
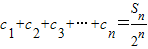
=
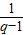
[
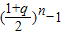
].再利用数列Tn与cn的关系求出c
n=

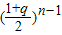
,从而易证{c
n}是等比数列.
解答:解:(1)
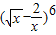
展开式的通项为
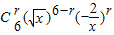
=
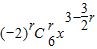
,令3-

r=0,r=2,
常数项为(-2)
2C
62=60,a
1=1,在
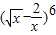
展开式中令x=1,得出各项系数和为(1-2)
6=1,即d=1.a
n=n.
①S
2=C
21+2C
22=4,S
3=C
31+2C
32+3C
33=12,S
4=C
41+2C
42+3C
43+4C
44=32
②S
n=

b
n∵S
n=C
n1+2C
n2+3C
n3+4C
n4+…+nC
nn
又 S
n=nC
nn+(n-1)C
n n-1+(n-2)C
n n-2+(n-3)C
n n-3+…+C
n1
两式相加得2S
n=C
n1+n(C
n1+C
n2+C
n3+C
n4+…+C
nn-1)+nC
nn=n(2n-C
n-C
nn)+2n=n•2
n=b
n
∴S
n=

b
n.
(2)∵a
kC
nk=
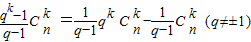
∴S
n=
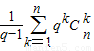
-
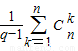
=
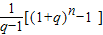
-
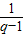
(2
n-1)=
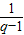
[(1+q)
n-2
n].
∴T
n=
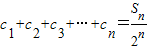
=
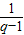
[
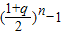
].
当n=1时,c
1=T
1=
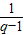
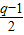
=

.
当n≥2时 c
n=T
n-T
n-1=
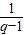
[
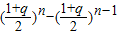
]=

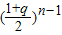
,对n=1时也成立.
∴c
n=

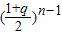
,{c
n}是以

为首项,以
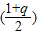
为公比的等比数列.
点评:重点考察二项式定理的应用,解决的方法有倒序相加法求和,利用数列和的定义求通项,难点在于综合分析,配凑逆用二项式定理,属于难题.考查计算、化简能力.

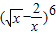 展开式的常数项的
展开式的常数项的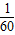 ,公差d为
,公差d为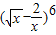 展开式的各项系数和①求S2,S3,S4,②找出Sn与bn的关系,并说明理由.
展开式的各项系数和①求S2,S3,S4,②找出Sn与bn的关系,并说明理由.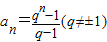 ,且数列{cn}满足
,且数列{cn}满足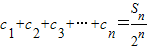 ,求证:{cn}是等比数列.
,求证:{cn}是等比数列. bn,再用倒序相加法证明.
bn,再用倒序相加法证明.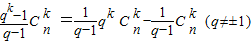 ,利用分组法,结合二项式定理的逆用、二项式系数的性质,求出 Tn=
,利用分组法,结合二项式定理的逆用、二项式系数的性质,求出 Tn=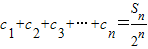 =
=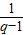 [
[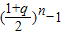 ].再利用数列Tn与cn的关系求出cn=
].再利用数列Tn与cn的关系求出cn=
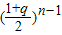 ,从而易证{cn}是等比数列.
,从而易证{cn}是等比数列.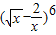 展开式的通项为
展开式的通项为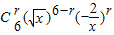 =
=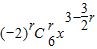 ,令3-
,令3- r=0,r=2,
r=0,r=2,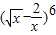 展开式中令x=1,得出各项系数和为(1-2)6=1,即d=1.an=n.
展开式中令x=1,得出各项系数和为(1-2)6=1,即d=1.an=n. bn
bn bn.
bn.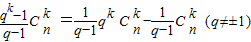
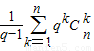 -
-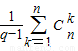 =
=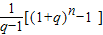 -
-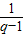 (2n-1)=
(2n-1)=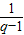 [(1+q)n-2n].
[(1+q)n-2n].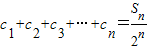 =
=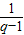 [
[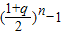 ].
].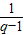
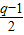 =
= .
.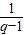 [
[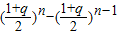 ]=
]=
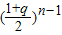 ,对n=1时也成立.
,对n=1时也成立.
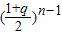 ,{cn}是以
,{cn}是以 为首项,以
为首项,以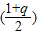 为公比的等比数列.
为公比的等比数列.
