
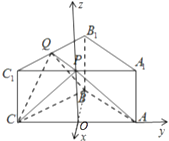
【题目】如图,ABC﹣A1B1C1是底面边长为2,高为 ![]() 的正三棱柱,经过AB的截面与上底面相交于PQ,设C1P=λC1A1(0<λ<1).、
的正三棱柱,经过AB的截面与上底面相交于PQ,设C1P=λC1A1(0<λ<1).、 
(1)证明:PQ∥A1B1;
(2)当 ![]() 时,求点C到平面APQB的距离.
时,求点C到平面APQB的距离.
【答案】
(1)证明:∵平面ABC∥平面A1B1C1,平面ABC∩平面ABQP=AB,平面ABQP∩平面A1B1C1=QP,
∴AB∥PQ,
又∵AB∥A1B1,
∴PQ∥A1B1.
(2)解:建立如图所示的直角坐标系.
∴O(0,0,0),P(0,0, ![]() ),A(0,1,0),B(﹣
),A(0,1,0),B(﹣ ![]() ,0,0),C(0,﹣1,0),
,0,0),C(0,﹣1,0),
∴ ![]() =(0,﹣1,
=(0,﹣1, ![]() ),
), ![]() =(﹣
=(﹣ ![]() ,﹣1,0),
,﹣1,0), ![]() =(0,﹣2,0),
=(0,﹣2,0),
设平面APQB的法向量为 ![]() =(x,y,z),
=(x,y,z),
则  ,可得
,可得 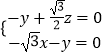 ,
,
取 ![]() =
= ![]() ,
,
∴点C到平面APQB的距离d= ![]() =
= ![]() =
= ![]() .
.
【解析】(1)由平面ABC∥平面A1B1C1 , 利用线面平行的性质定理可得:AB∥PQ,又AB∥A1B1 , 即可证明PQ∥A1B1 . (2)建立如图所示的直角坐标系.设平面APQB的法向量为 ![]() =(x,y,z),则
=(x,y,z),则  ,利用点C到平面APQB的距离d=
,利用点C到平面APQB的距离d= ![]() 即可得出.
即可得出.
【考点精析】解答此题的关键在于理解棱柱的结构特征的相关知识,掌握两底面是对应边平行的全等多边形;侧面、对角面都是平行四边形;侧棱平行且相等;平行于底面的截面是与底面全等的多边形.


 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() ,过点
,过点![]() ,
,![]() 的直线倾斜角为
的直线倾斜角为![]() ,原点到该直线的距离为
,原点到该直线的距离为![]() .
.
(Ⅰ)求椭圆的标准方程;
(Ⅱ)斜率大于零的直线过![]() 与椭圆交于E,F两点,若
与椭圆交于E,F两点,若![]() ,求直线EF的方程.
,求直线EF的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面上,我们如果用一条直线去截正方形的一个角,那么截下的一个直角三角形,按图所标边长,由勾股定理有:c2=a2+b2。设想正方形换成正方体,把截线换成如下图的截面,这时从正方体上截下三条侧棱两两垂直的三棱锥O![]() LMN,如果用S1,S2,S3表示三个侧面面积,S4表示截面面积,那么你类比得到的结论是 .
LMN,如果用S1,S2,S3表示三个侧面面积,S4表示截面面积,那么你类比得到的结论是 .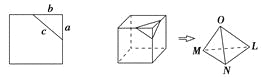
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,
中,![]() 是等腰三角形,且
是等腰三角形,且![]() .四边形
.四边形![]() 是直角梯形,
是直角梯形,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.

(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)当平面![]()
![]() 平面
平面![]() 时,求四棱锥
时,求四棱锥![]() 的体积;
的体积;
(Ⅲ)请在图中所给的五个点![]() 中找出两个点,使得这两点所在的直线与直线
中找出两个点,使得这两点所在的直线与直线![]() 垂直,并给出证明.
垂直,并给出证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线l的参数方程为  ( t为参数).以原点为极点,x轴正半轴为极轴 建立极坐标系,圆C的方程为 ρ=2
( t为参数).以原点为极点,x轴正半轴为极轴 建立极坐标系,圆C的方程为 ρ=2 ![]() sinθ.
sinθ.
(1)写出直线l的普通方程和圆C的直角坐标方程;
(2)若点P的直角坐标为(1,0),圆C与直线l交于A,B两点,求|PA|+|PB|的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数f(x)在区间A上,对a,b,c∈A,f(a),f(b),f(c)为一个三角形的三边长,则称函数f(x)为“三角形函数”.已知函数f(x)=xlnx+m在区间[ ![]() ,e]上是“三角形函数”,则实数m的取值范围为( )
,e]上是“三角形函数”,则实数m的取值范围为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义域为R的偶函数f(x)满足对x∈R,有f(x+2)=f(x)﹣f(1),且当x∈[2,3]时,f(x)=﹣2x2+12x﹣18,若函数y=f(x)﹣loga(|x|+1)在(0,+∞)上至少有三个零点,则a的取值范围是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题p:m∈R,使得函数f(x)=x2+(m﹣1)x2﹣2是奇函数,命题q:向量 ![]() =(x1 , y1),
=(x1 , y1), ![]() =(x2 , y2),则“
=(x2 , y2),则“ ![]() =
= ![]() ”是:“
”是:“ ![]()
![]() ”的充要条件,则下列命题为真命题的是( )
”的充要条件,则下列命题为真命题的是( )
A.p∧q
B.(¬p)∧q
C.p∧(¬q)
D.(¬p)∧(¬q)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com