练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    当m>1时，关于x的不等式x2+(m-1)x-m≥0的解集是


    1. A.
      {x|x≤1，或x≥-m}
    2. B.
      {x|1≤x≤-m }
    3. C.
      {x|x≤-m，或x≥1}
    4. D.
      {x|-m≤x≤1 }
    C
    试题分析：根据题意可知，原不等式可化为 （x+m）（x-1）0，结合一元二次不等式的解法，求出它的解集，解得为，因此可知结论为{x|x≤-m，或x≥1}，选C.
    考点：不等式的解集
    点评：本题主要考查一元二次不等式的解法，属于基础题
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    给出下列四个命题：

    ①当x>0且x≠1时，有lnx＋??2；     ②函数f(x)＝lg(ax+1)的定义域为{x|x> }；

    ③函数f(x)＝e-xx2在x＝2上取得极大值；

    ④x2+y2-10x+4y-5＝0上的任意点M关于直线ax-y-5a-2＝0对称点M/也在该圆上.

    所有正确命题的序号是           .（把你认为正确命题的序号都填上）

    查看答案和解析>>

    科目：高中数学 来源：2011年福建省罗源县第一中学高二上学期期中考试理科数学 题型：解答题

    已知f(x)=-3x2+m(6-m)x+n
    （1）    解关于m的不等式f(1)>0；
    （2）    当不等式f(x)>0的解集为（-1，3）时，求实数m，n的值。

    查看答案和解析>>

    科目：高中数学 来源：2014届辽宁沈阳四校协作体高二上学期期中考试理数学试卷（解析版） 题型：选择题

    当m>1时，关于x的不等式x2+(m-1)x-m≥0的解集是

    A．{x|x≤1，或x≥-m}                     B． {x|1≤x≤-m }

    C．{x|x≤-m，或x≥1}                     D． {x|-m≤x≤1 }

     

    查看答案和解析>>

    科目：高中数学 来源：2014届吉林省高一上学期期末考试数学 题型：解答题

    （本小题满分12分）

    已知函数f(x)=log a 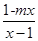(a>0且a≠1)的图像关于原点对称

    （1）求m的值；  

    （2）判断函数f(x)在区间（1，+∞）上的单调性并加以证明；

    （3）当a>1，x∈(t,a)时, f(x)的值域是（1，+∞），求a与t的值。

     

     

    查看答案和解析>>

    同步练习册答案