
【题目】已知直线![]() 经过抛物线
经过抛物线![]() 的焦点且与此抛物线交于
的焦点且与此抛物线交于![]() ,
,![]() 两点,
两点,![]() ,直线
,直线![]() 与抛物线
与抛物线![]() 交于
交于![]() ,
,![]() 两点,且
两点,且![]() ,
,![]() 两点在
两点在![]() 轴的两侧.
轴的两侧.
(1)证明:![]() 为定值;
为定值;
(2)求直线![]() 的斜率的取值范围;
的斜率的取值范围;
(3)若![]() (
(![]() 为坐标原点),求直线
为坐标原点),求直线![]() 的方程.
的方程.
【答案】(1)见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】分析:(1)可设l的方程为y=k(x﹣1),k≠0,联立![]() ,可得ky2﹣4y﹣4k=0,根据韦达定理即可证明,
,可得ky2﹣4y﹣4k=0,根据韦达定理即可证明,
(2)根据韦达定理和抛物线的性质可得k2>1,再联立![]() ,得x2﹣kx+k﹣4=0,根据M,N两点在y轴的两侧,可得△=k2﹣4(k﹣4)>0,即k<4,即可求出k的范围,
,得x2﹣kx+k﹣4=0,根据M,N两点在y轴的两侧,可得△=k2﹣4(k﹣4)>0,即k<4,即可求出k的范围,
(3)设![]() ,
,![]() ,则
,则![]() ,
,![]() ,利用根与系数关系表示
,利用根与系数关系表示![]() ,即可得到直线
,即可得到直线![]() 的方程.
的方程.
详解:(1)证明:由题意可得,直线![]() 的斜率存在,故可设
的斜率存在,故可设![]() 的方程为
的方程为![]() ,
,
联立![]() ,得
,得![]() ,则
,则![]() 为定值.
为定值.
(2)解:由(1)知,![]() ,
,![]()
![]() ,
,
则![]()
![]()
![]() ,即
,即![]() .
.
联立![]() ,得
,得![]() ,
,
∵![]() ,
,![]() 两点在
两点在![]() 轴的两侧,∴
轴的两侧,∴![]()
![]() ,且
,且![]() ,∴
,∴![]() .
.
由![]() 及
及![]() 可得
可得![]() 或
或![]() ,
,
故直线![]() 的斜率的取值范围为
的斜率的取值范围为![]() .
.
(3)解:设![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,
∴![]()
![]()
![]()
![]()
![]() ,
,
解得![]() 或
或![]() ,又
,又![]() ,∴
,∴![]() ,
,
故直线![]() 的方程为
的方程为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,
,![]() 是椭圆
是椭圆![]() 上在第二象限内的一点,且直线
上在第二象限内的一点,且直线![]() 的斜率为
的斜率为![]() .
.
(1)求![]() 点的坐标;
点的坐标;
(2)过点![]() 作一条斜率为正数的直线
作一条斜率为正数的直线![]() 与椭圆
与椭圆![]() 从左向右依次交于
从左向右依次交于![]() 两点,是否存在实数
两点,是否存在实数![]() 使得
使得![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国是世界上严重缺水的国家,某市政府为了鼓励居民节约用水,计划调整居民生活用水收费方案,拟确定一个合理的月用水量标准![]() (吨)、一位居民的月用水量不超过
(吨)、一位居民的月用水量不超过![]() 的部分按平价收费,超出
的部分按平价收费,超出![]() 的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),…,[4,4.5]分成9组,制成了如图所示的频率分布直方图.
的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),…,[4,4.5]分成9组,制成了如图所示的频率分布直方图.

(Ⅰ)求直方图中a的值;
(Ⅱ)设该市有30万居民,估计全市居民中月均用水量不低于3吨的人数,并说明理由;
(Ⅲ)若该市政府希望使85%的居民每月的用水量不超过标准![]() (吨),估计
(吨),估计![]() 的值,并说明理由.
的值,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】人的卷舌与平舌(指是否能左右卷起来)同人的眼皮单双一样,也是由遗传自父母的基因决定的,其中显性基因记作D,隐性基因记作d;成对的基因中,只要出现了显性基因,就一定是卷舌的(这就是说,“卷舌”的充要条件是“基因对是![]() ,
,![]() 或
或![]() ”).同前面一样,决定眼皮单双的基因仍记作B(显性基因)和b(隐性基因).
”).同前面一样,决定眼皮单双的基因仍记作B(显性基因)和b(隐性基因).
有一对夫妻,两人决定舌头形态和眼皮单双的基因都是![]() ,不考虑基因突变,求他们的孩子是卷舌且单眼皮的概率.(有关生物学知识表明:控制上述两种不同性状的基因遗传时互不干扰).
,不考虑基因突变,求他们的孩子是卷舌且单眼皮的概率.(有关生物学知识表明:控制上述两种不同性状的基因遗传时互不干扰).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]()
![]() ,过直线
,过直线![]() :
:![]() 上任一点
上任一点![]() 向抛物线
向抛物线![]() 引两条切线
引两条切线![]() (切点为
(切点为![]() ,且点
,且点![]() 在
在![]() 轴上方).
轴上方).
(1)求证:直线![]() 过定点,并求出该定点;
过定点,并求出该定点;
(2)抛物线![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数,![]() ),曲线
),曲线![]() 的参数方程为
的参数方程为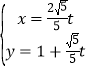 (
(![]() 为参数,且
为参数,且![]() ).
).
(1)以曲线![]() 上的点与原点
上的点与原点![]() 连线的斜率
连线的斜率![]() 为参数,写出曲线
为参数,写出曲线![]() 的参数方程;
的参数方程;
(2)若曲线![]() 与
与![]() 的两个交点为
的两个交点为![]() ,直线
,直线![]() 与直线
与直线![]() 的斜率之积为
的斜率之积为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知倾斜角为
中,已知倾斜角为![]() 的直线
的直线![]() 经过点
经过点![]() .以坐标原点
.以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]()
(1)写出曲线![]() 的普通方程;
的普通方程;
(2)若直线![]() 与曲线
与曲线![]() 有两个不同的交点
有两个不同的交点![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某生产企业对其所生产的甲、乙两种产品进行质量检测,分别各抽查6件产品,检测其重量的误差,测得数据如下(单位:![]() ):
):
甲:13 15 13 8 14 21
乙:15 13 9 8 16 23
(1)画出样本数据的茎叶图;
(2)分别计算甲、乙两组数据的方差并分析甲、乙两种产品的质量(精确到0.1)。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com