
如图所示,已知![]() 中,
中,![]() AB=2OB=4,若
AB=2OB=4,若![]() 是
是![]() 绕直线AO旋转而成的,记二面角B—AO—C的大小为
绕直线AO旋转而成的,记二面角B—AO—C的大小为![]()
(I)若![]() ,求证:平面
,求证:平面![]() 平面AOB;
平面AOB;
(II)若![]() 时,求二面角C—OD—B的余弦值的最小值。
时,求二面角C—OD—B的余弦值的最小值。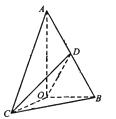
【解】解法一:(I)如图所示,以O为原点,在平面OBC内垂直于OB的直线为x轴,
OB,OA所在的直线分别为y轴,z轴建立空间直角坐标系O-xyz,
则A(0,0,2![]() ),B(0,2,0),D(0,1,
),B(0,2,0),D(0,1,![]() ),C(2sinθ,2cosθ,0).
),C(2sinθ,2cosθ,0).

(II)设二面角C-OD-B的大小为α,由(1)得
当θ=![]() 时,cosα=0;当θ∈(
时,cosα=0;当θ∈(![]() ,
,![]() ]时,tanθ≤-
]时,tanθ≤-![]() ,
,
cosα=![]() =
=![]() =-
=-![]() ,……10分
,……10分
故-![]() ≤cosα<0.因此cosα的最小值为-
≤cosα<0.因此cosα的最小值为-![]() ,
,
 综上,二面角C-OD-B的余弦值的最小值为-
综上,二面角C-OD-B的余弦值的最小值为-![]() . ……13分
. ……13分
解法二:(I)因为AO⊥OB,二面角B-AO-C为![]() , ……3分
, ……3分
所以OB⊥OC,又OC⊥OA,所以OC⊥平面AOB
所以平面AOB⊥平面CO D. ……6分
(II)当θ=![]() 时,二面角C-OD-B的余弦值为0;……7分
时,二面角C-OD-B的余弦值为0;……7分
当θ∈(![]() ,
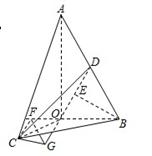
,![]() ]时,过B作OD的垂线,垂足为E,
]时,过B作OD的垂线,垂足为E,
过C作OB的垂线,垂足为F,过F作OD的垂线,垂足为G,连结CG,
则∠CGF的补角为二面角C-OD-B的平面角.
在Rt△OCF中,CF=2sinθ,OF=-2cosθ,
在Rt△CGF中,GF=OFsin![]() =-
=-![]() cosθ,CG=
cosθ,CG=![]() ,
,
所以cos∠CGF=![]() =-
=-![]() . ……10分
. ……10分
因为θ∈(![]() ,
,![]() ],tanθ≤-
],tanθ≤-![]() ,故0<cos∠CGF=
,故0<cos∠CGF=![]() ≤
≤![]() .
.
所以二面角C-OD-B的余弦值的最小值为-![]() . ……13分
. ……13分


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
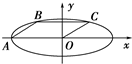 如图所示,已知椭圆的方程为
如图所示,已知椭圆的方程为| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
查看答案和解析>>
科目:高中数学 来源: 题型:
 随机抽查某中学高三年级100名学生的视力情况,得其频率分布直方图如图所示.已知前4组的频数成等比数列,后6组的频数成等差数列,则视力在4.6到5.0之间的学生人数为( )
随机抽查某中学高三年级100名学生的视力情况,得其频率分布直方图如图所示.已知前4组的频数成等比数列,后6组的频数成等差数列,则视力在4.6到5.0之间的学生人数为( )查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com