
(1)求这位挑战者总得分ξ不为负分(即ξ≥0)的概率;
(2)求这位挑战者回答这两个问题的总得分的概率分布和数学期望.
解:(1)如果两个题目均答错,得0+(-10)=-10分.
P(ξ=-10)=0.2×0.4=0.08.
这位挑战者总得分不为负分的概率为
P(ξ≥0)=1-P(ξ<0)=1-0.08=0.92.
(2)如果两个题目均答错,得0+(-10)=-10分.
如果两个题目一对一错,包括两种情况:
①第一个对,第二个错,得10+(-10)=0分;
②第一个错,第二个对,得0+20=20分,
如果两个题目均答对,得10+20=30分.
故ξ的可能取值为-10,0,20,30.
P(ξ=-10)=0.2×0.4=0.08;P(ξ=0)=0.8×0.4=0.32;
P(ξ=20)=0.2×0.6=0.12;P(ξ=30)=0.8×0.6=0.48.
所以ξ的概率分布为
ξ | -10 | 0 | 20 | 30 |
P | 0.08 | 0.32 | 0.12 | 0.48 |
根据ξ的概率分布,可得ξ的期望:
Eξ=(-10)×0.08+0×0.32+20×0.12+30×0.48=16.


科目:高中数学 来源: 题型:
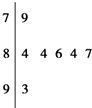 如图是某电视台综艺节目举办的挑战主持人大赛上,七位评委为某选手打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为( )
如图是某电视台综艺节目举办的挑战主持人大赛上,七位评委为某选手打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为( )| A、84,4.84 | B、84,1.6 | C、85,4 | D、85,1.6 |
查看答案和解析>>
科目:高中数学 来源: 题型:
(1)求这位挑战者回答这两个问题的总得分分别为-10分、20分的概率;
(2)求这位挑战者总得分不为负分的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com