Question

（09年西城区抽样文）（14分）

已知的顶点A在射线上， A, B两点关于x轴对称，O为坐标原点，且线段AB上有一点M满足. 当点A在l₁上移动时，记点M的轨迹为W.

    (Ⅰ) 求轨迹W的方程；

    (Ⅱ) 设N(2,0)，过N的直线l与W相交于P、Q两点. 求证：不存在直线l，使得.

Answer 1

解析：（Ⅰ）解：因为A, B两点关于x轴对称，

         所以AB边所在直线与y轴平行.          

设M(x, y)，由题意，得，           ---------------------2分

     所以，                    

因为，

所以，即，          ---------------------5分

所以点M的轨迹W的方程为.            ------------------6分

  （Ⅱ）证明：设或，，

     当直线时：

         由题意，知点P，Q的坐标是方程组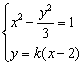的解，

         消去y得，

         所以，且，

             ，                  ------------8分

             因为直线l与双曲线的右支（即W)相交两点P、Q，

             所以，即.     1----9分

因为，

所以，                         

                       ，

                       

，                        --------------------11分

       要使，则必须有，解得，代入1不符合. --12分

                 所以不存在l，使得.

        当直线时，P(2, 3)，，，不符合题意.

        综上：不存在直线l使得.                   ------------------14分