Question

（（本题14分）如图3，四棱锥P—ABCD中，底面ABCD是矩形，PA⊥平面ABCD，M、N分别是AB、PC的中点，PA=AD=。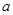

  (Ⅰ)求证：MN//平面PAD；

  (Ⅱ)求证：平面PMC⊥平面PCD；

  (Ⅲ)若二面角P—MC—A是60°的二面角，求四棱锥P—ABCD的体积。

 

 

 

 

                                                                

 

 

 

Answer 1

【答案】

 

证明：(Ⅰ)如答图所示，⑴设PD的中点为E，连结AE、NE，

 

 

由N为PD的中点知ENDC，

又ABCD是矩形，∴DCAB，∴ENAB

又M是AB的中点，∴ENAN，                       …3分

∴AMNE是平行四边形

∴MN∥AE，而AE平面PAD，NM平面PAD

∴MN∥平面PAD                                    …4分

(Ⅱ)∵PA＝AD，∴AE⊥PD，

又∵PA⊥平面ABCD，CD平面ABCD，

∴CD⊥PA，而CD⊥AD，∴CD⊥平面PAD                                 …6分

∴CD⊥AE， ∵PD∩CD＝D，∴AE⊥平面PCD，                          

∵MN∥AE，∴MN⊥平面PCD，又MN平面PMC，

∴平面PMC⊥平面PCD.                                                …8分

　（Ⅲ）解：过A作AH⊥CM，交CM的延长线于H，连PH．

　　∵PA⊥平面ABCD，AH⊥CH，∴PH⊥CH，     ∴∠PHA是二面角P－MC－A的平面角，

∴AH＝                                          …   10分

　　又∵Rt△MHA∽Rt△MBC，

　　

∴     　 …12分

∴                                 …14分

解法二：(Ⅱ)以A为原点，AB,AD,AP所在直线分别为轴、轴、轴建系

设AB=b   (b>0)      面PMC法向量  面PDC法向量

∵          ∴面PMC面PDC                          …8分

（Ⅲ）面MCA法向量        ∵二面角P—MC—A是60°的二面角

∴                          ∴        …12分

∴                       …14分

 

【解析】略