
【题目】对于函数![]() ,若存在
,若存在![]() ,使
,使![]() 成立,则称
成立,则称![]() 为函数
为函数![]() 的不动点,已知
的不动点,已知![]() .
.
(1)若![]() 有两个不动点为
有两个不动点为![]() ,求函数
,求函数![]() 的零点;
的零点;
(2)若![]() 时,函数
时,函数![]() 没有不动点,求实数
没有不动点,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)由不动点的定义可知: ![]() 为
为![]() 两根,结合根与系数关系可求得
两根,结合根与系数关系可求得![]() 的值;易得函数
的值;易得函数![]() ,令
,令![]() , 求出方程的根,从而可求得函数
, 求出方程的根,从而可求得函数![]() 的零点;(2)由函数
的零点;(2)由函数![]() 没有不动点可得方程
没有不动点可得方程![]() 无实数根,由
无实数根,由![]() 即可求得实数
即可求得实数![]() 的取值范围.
的取值范围.
试题解析:(1)由题意知:f(x)=x,即x2+(b-1)x+c=0有两根,分别为-3,2.
所以![]() ,所以
,所以![]() ,从而f(x)=x2+2x-6,
,从而f(x)=x2+2x-6,
由f(x)=0得x1=-1-![]() ,x2=-1+
,x2=-1+![]() .
.
故f(x)的零点为-1±![]() .
.
(2)若c=![]() ,则f(x)=x2+bx+
,则f(x)=x2+bx+![]() ,
,
又f(x)无不动点,
即方程x2+bx+![]() =x无解,
=x无解,
所以(b-1)2-b2<0.
即-2b+1<0,所以b>![]() .故b的取值范围是b>
.故b的取值范围是b>![]() .
.


科目:高中数学 来源: 题型:
【题目】已知函数![]()
![]() 的图象过点
的图象过点![]() 。
。
(1)求![]() 的值并求函数
的值并求函数![]() 的值域;
的值域;
(2)若关于![]() 的方程
的方程![]() 有实根,求实数
有实根,求实数![]() 的取值范围;
的取值范围;
(3)若函数![]() ,
, ![]() ,则是否存在实数
,则是否存在实数![]() ,使得函数
,使得函数![]() 的最大值为0?若存在,求出
的最大值为0?若存在,求出![]() 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 与函数
与函数![]() 的图像相切于点
的图像相切于点![]() .
.
(1)求实数![]() 的值;
的值;
(2)证明除切点![]() 外,直线
外,直线![]() 总在函数
总在函数![]() 的图像的上方;
的图像的上方;
(3)设![]() 是两两不相等的正实数,且
是两两不相等的正实数,且![]() 成等比数列,试判断
成等比数列,试判断![]() 与
与![]() 的大小关系,并证明你的结论.
的大小关系,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某投资人欲将5百万元奖金投入甲、乙两种理财产品,根据银行预测,甲、乙两种理财产品的收益与投入奖金![]() 的关系式分别为
的关系式分别为![]() ,其中
,其中![]() 为常数且
为常数且![]() .设对乙种产品投入奖金
.设对乙种产品投入奖金![]() 百万元,其中
百万元,其中![]() .
.
(1)当![]() 时,如何进行投资才能使得总收益
时,如何进行投资才能使得总收益![]() 最大;(总收益
最大;(总收益![]() )
)
(2)银行为了吸储,考虑到投资人的收益,无论投资人奖金如何分配,要使得总收益不低于![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=ln x-ax(a∈R)(e=2.718 28…是自然对数的底数).
(1)判断f(x)的单调性;
(2)当f(x)<0在(0,+∞)上恒成立时,求a的取值范围;
(3)证明:当x∈(0,+∞)时,![]() (1+x)
(1+x) ![]() <e.
<e.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为创建全国文明城市,某区向各事业行政单位征集“文明过马路”义务督导员.从符合条件的600名志愿者中随机抽取100名,按年龄作分组如下:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,并得到如下频率分布直方图.
,并得到如下频率分布直方图.
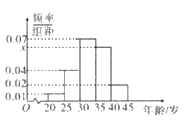
(I)求图中![]() 的值,并根据频率分布直方图统计这600名志愿者中年龄在
的值,并根据频率分布直方图统计这600名志愿者中年龄在![]() 的人数;
的人数;
(II)在抽取的100名志愿者中按年龄分层抽取5名参加区电视台“文明伴你行”节目录制,再从这5名志愿者中随机抽取2名到现场分享劝导制止行人闯红灯的经历,求至少有1名年龄不低于35岁的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班同学利用国庆节进行社会实践,对[25,55]岁的人群随机抽取![]() 人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率分布直方图:
人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率分布直方图:
组数 | 分组 | 低碳族的人数 | 占本组的频率 |
第一组 | [25,30) | 120 | 0.6 |
第二组 | [30,35) | 195 |
|
第三组 | [35,40) | 100 | 0.5 |
第四组 | [40,45) |
| 0.4 |
第五组 | [45,50) | 30 | 0.3 |
第六组 | [50,55] | 15 | 0.3 |
(1)补全频率分布直方图并求![]() 的值;
的值;
(2)从年龄段在[40,50)的“低碳族”中采用分层抽样法抽取6人参加户外低碳体验活动,其中选取2人作为领队,求选取的2名领队中恰有1人年龄在[4,45)岁的概率.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com