
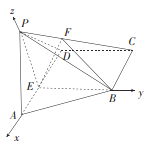
【题目】如图,四棱锥![]() 中,侧面
中,侧面![]() 底面
底面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,点
,点![]() 在棱
在棱![]() 上,且
上,且![]() ,点
,点![]() 在棱
在棱![]() 上,且
上,且![]() 平面
平面![]() .
.
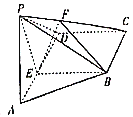
(1)求证: ![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)详见解析(2)![]()
【解析】试题分析:连接![]() 交
交![]() 于点
于点![]() ,根据三角形相识,可得
,根据三角形相识,可得![]() ,
, ![]() ,由勾股定理可得
,由勾股定理可得![]() 是直角三角形,进而得
是直角三角形,进而得![]() ,再由面面垂直判定定理可得结论;(2)以
,再由面面垂直判定定理可得结论;(2)以![]() ,
, ![]() ,
, ![]() 所在直线分别为
所在直线分别为![]() 轴,
轴, ![]() 轴,
轴, ![]() 轴建立空间直角坐标系,求出平面
轴建立空间直角坐标系,求出平面![]() 的法向量与平面
的法向量与平面![]() 的法向量,利用空间向量夹角余弦公式可得结果.
的法向量,利用空间向量夹角余弦公式可得结果.
试题解析:(1)如图连接![]() 交
交![]() 于点
于点![]() ,因为
,因为![]() 平面
平面![]() ,所以
,所以![]() ,由
,由![]() ,所以
,所以![]() ,又
,又![]() ,所以
,所以![]() ,
,
所以![]() ,
, ![]() ,
,
又因为![]() ,所以
,所以![]() 是直角三角形,
是直角三角形,
又![]() ,所以
,所以![]() ,
,
又因为侧面![]() 底面
底面![]() ,所以
,所以![]() 平面
平面![]() .
.
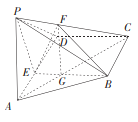
(2)因为![]() ,
, ![]() ,所以
,所以![]() ,有
,有![]() ,如图,以
,如图,以![]() ,
, ![]() ,
, ![]() 所在直线分别为
所在直线分别为![]() 轴,
轴, ![]() 轴,
轴, ![]() 轴建立空间直角坐标系,
轴建立空间直角坐标系,
则![]() ,
, ![]() ,
, ![]() ,
,
![]() ,所以
,所以![]() ,
,
所以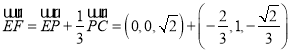
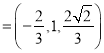 ,
,
设平面![]() 的法向量为
的法向量为![]() ,
,
则![]() ,
,
![]() ,令
,令![]() ,则
,则![]() ,所以
,所以![]() ,
,
又因为平面![]() 的法向量
的法向量![]() ,
,
所以![]() ,
,
即所求二面角的余弦值是![]() .
.


科目:高中数学 来源: 题型:
【题目】已知数列{an}满足a1=9,an+1=an+2n+5;数列{bn}满足b1= ![]() ,bn+1=
,bn+1= ![]() bn(n≥1).
bn(n≥1).
(1)求an , bn;
(2)记数列{ ![]() }的前n项和为Sn , 证明:
}的前n项和为Sn , 证明: ![]() ≤Sn<
≤Sn< ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《中国诗词大会》是中央电视台最近推出的一档有重大影响力的大型电视文化节目,今年两会期间,教育部部长陈宝生答记者问时就给予其高度评价.基于这样的背景,山东某中学积极响应,也举行了一次诗词竞赛.组委会在竞赛后,从中抽取了部分选手的成绩(百分制),作为样本进行统计,作出了图1的频率分布直方图和图2的茎叶图(但中间三行污损,看不清数据).
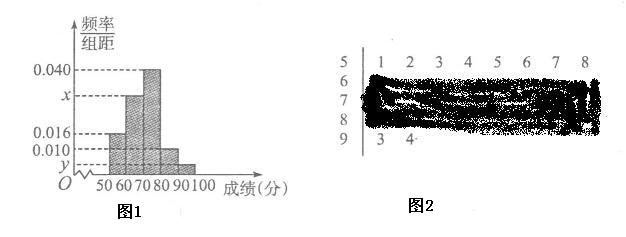
(I)求样本容量![]() 和频率分布直方图中的
和频率分布直方图中的![]() ,
,![]() 的值;
的值;
(II)分数在[80,90)的学生中,男生有2人,现从该组抽取三人“座谈”,写出基本事件空间并求至少有两名女生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知抛物线![]() :
:![]() ,过焦点
,过焦点![]() 斜率大于零的直线
斜率大于零的直线![]() 交抛物线于
交抛物线于![]() 、
、![]() 两点,且与其准线交于点
两点,且与其准线交于点![]() .
.

(Ⅰ)若线段![]() 的长为
的长为![]() ,求直线
,求直线![]() 的方程;
的方程;
(Ⅱ)在![]() 上是否存在点
上是否存在点![]() ,使得对任意直线
,使得对任意直线![]() ,直线
,直线![]() ,
,![]() ,
,![]() 的斜率始终成等差数列,若存在求点
的斜率始终成等差数列,若存在求点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4;坐标系与参数方程
在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).在以坐标原点为极点,
为参数).在以坐标原点为极点, ![]() 轴正半轴为极轴的极坐标中,曲线
轴正半轴为极轴的极坐标中,曲线![]() .
.
(Ⅰ)求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程.
的直角坐标方程.
(Ⅱ)求曲线![]() 上的点到直线
上的点到直线![]() 的距离的最大值.
的距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]() 为实常数.
为实常数.
(Ⅰ)设![]() ,当
,当![]() 时,求函数
时,求函数![]() 的单调区间;
的单调区间;
(Ⅱ)当![]() 时,直线
时,直线![]() 、
、![]() 与函数
与函数![]() 、
、![]() 的图象一共有四个不同的交点,且以此四点为顶点的四边形恰为平行四边形.
的图象一共有四个不同的交点,且以此四点为顶点的四边形恰为平行四边形.
求证: ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com