
【题目】已知圆心在![]() 轴上的圆
轴上的圆![]() 与直线
与直线![]() 切于点
切于点![]() .
.
(1)求圆![]() 的标准方程;
的标准方程;
(2)已知![]() ,经过原点,且斜率为正数的直线
,经过原点,且斜率为正数的直线![]() 与圆
与圆![]() 交于
交于![]() 两点.
两点.
(ⅰ)求证: ![]() 为定值;
为定值;
(ⅱ)求![]() 的最大值.
的最大值.
【答案】(1)![]() ;(2)(ⅰ)见解析;(ⅱ)
;(2)(ⅰ)见解析;(ⅱ)![]() .
.
【解析】试题分析:(1)由题意可知, ![]() ,解得
,解得![]() ,可求得半径
,可求得半径![]() ,得圆的方程.
,得圆的方程.
(2)(i)设直线l的方程为![]() ,与圆的方程联立,可得
,与圆的方程联立,可得![]() ,利用韦达定理即可证明;
,利用韦达定理即可证明;
(ii)表示 ![]()
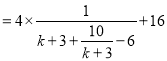 再求最值即可.
再求最值即可.
试题解析:(1)设圆心![]() 的坐标为
的坐标为![]() ,则
,则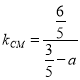 ,又
,又![]() ,
,
由题意可知, ![]() ,则
,则![]() ,
,
故![]() ,所以
,所以![]() ,即半径
,即半径![]() .
.
故圆![]() 的标准方程为
的标准方程为![]() .
.
(2)设直线![]() 的方程为
的方程为![]() ,
,
由![]() 得:
得: ![]() ,
,
所以![]() ,
, ![]() .
.
(ⅰ)![]() 为定值,
为定值,
(ⅱ)![]()
![]()
![]()
![]()
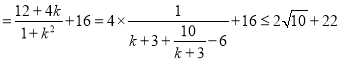
(当且仅当![]() ,即
,即![]() 时等号成立)
时等号成立)
故![]() 的最大值为
的最大值为![]() .
.
点睛:本题主要考查直线与圆锥曲线位置关系,所使用方法为韦达定理法:因直线的方程是一次的,圆锥曲线的方程是二次的,故直线与圆锥曲线的问题常转化为方程组关系问题,最终转化为一元二次方程问题,故用韦达定理及判别式是解决圆锥曲线问题的重点方法之一,尤其是弦中点问题,弦长问题,可用韦达定理直接解决,但应注意不要忽视判别式的作用.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知 ![]() =(
=( ![]() sinx,m+cosx),
sinx,m+cosx), ![]() =(cosx,﹣m+cosx),且f(x)=
=(cosx,﹣m+cosx),且f(x)= ![]()
(1)求函数f(x)的解析式;
(2)当x∈[﹣ ![]() ,
, ![]() ]时,f(x)的最小值是﹣4,求此时函数f(x)的最大值,并求出相应的x的值.
]时,f(x)的最小值是﹣4,求此时函数f(x)的最大值,并求出相应的x的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场为吸引顾客消费推出一项优惠活动.活动规则如下:消费额每满100元可转动如图所示的转盘一次,并获得相应金额的返券,假定指针等可能地停在任一位置.若指针停在A区域返券60元;停在B区域返券30元;停在C区域不返券.例如:消费218元,可转动转盘2次,所获得的返券金额是两次金额之和.

(1)若某位顾客消费128元,求返券金额不低于30元的概率;
(2)若某位顾客恰好消费280元,并按规则参与了活动,他获得返券的金额记为![]() (元).求随机变量
(元).求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
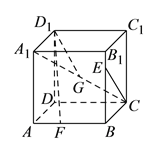
【题目】已知正方体![]() ,点
,点![]() ,
, ![]() ,
, ![]() 分别是线段
分别是线段![]() ,
, ![]() 和
和![]() 上的动点,观察直线
上的动点,观察直线![]() 与
与![]() ,
, ![]() 与
与![]() .给出下列结论:
.给出下列结论:
①对于任意给定的点![]() ,存在点
,存在点![]() ,使得
,使得![]() ;
;
②对于任意给定的点![]() ,存在点
,存在点![]() ,使得
,使得![]() ;
;
③对于任意给定的点![]() ,存在点
,存在点![]() ,使得
,使得![]() ;
;
④对于任意给定的点![]() ,存在点
,存在点![]() ,使得
,使得![]() .
.
其中正确结论的个数是( ).
A. ![]() 个 B.
个 B. ![]() 个 C.
个 C. ![]() 个 D.
个 D. ![]() 个
个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,已知内角 ![]() ,边
,边 ![]() .设内角B=x,△ABC的面积为y.
.设内角B=x,△ABC的面积为y.
(1)求函数y=f(x)的解析式和定义域;
(2)当角B为何值时,△ABC的面积最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图, ![]() 是半圆
是半圆![]() 的直径,
的直径, ![]() 是半圆
是半圆![]() 上除
上除![]() 、
、![]() 外的一个动点,
外的一个动点, ![]() 垂直于半圆
垂直于半圆![]() 所在的平面,
所在的平面, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
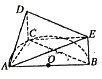
(1)证明:平面![]() 平面
平面![]() ;
;
(2)当三棱锥![]() 体积最大时,求二面角
体积最大时,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com